
如图,一次函数y=-x+b与反比例函数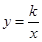 的图象相交于A(-1,4)、B(4,-1)两点,直线l⊥x轴于点E(-4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC
的图象相交于A(-1,4)、B(4,-1)两点,直线l⊥x轴于点E(-4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC

(1)、求出b和k;
(2)、求证:△ACD是等腰直角三角形;
(3)、在y轴上是否存在点P,使 ,若存在,请求出P的坐标,若不存在,请说明理由。
,若存在,请求出P的坐标,若不存在,请说明理由。
(1)3,-4;(2)证明见解析;(3)存在,P1(0, ),P2(0,-
),P2(0,- ).
).
【解析】
试题分析:(1)将已知点的坐标代入到两个函数的解析式即可求得k和b的值;
(2))根据直线x=-4与一次函数y=-x+3交于点D,求得点D(-4,7),根据直线x=-4与反比例函数y=- 交于点C确定点C(-4,1),从而确定AD=AC,然后根据勾股定理的逆定理确定△ACD是直角三角形,从而确定△ACD是等腰直角三角形;
交于点C确定点C(-4,1),从而确定AD=AC,然后根据勾股定理的逆定理确定△ACD是直角三角形,从而确定△ACD是等腰直角三角形;
(3)过点A作AP1∥BC,交y轴于P1,则S△PBC=S△ABC,根据B(4,-1),C(-4,1)确定直线BC的解析式为y=- x,然后设直线AP1的解析式为y=-
x,然后设直线AP1的解析式为y=- x+b1,把A(-1,4)代入可求b1=
x+b1,把A(-1,4)代入可求b1= ,求得P1(0,
,求得P1(0, ),作P1关于x轴的对称点P2,利用S△P1BC=S△P2BCBC=S△ABC,确定P2(0,-
),作P1关于x轴的对称点P2,利用S△P1BC=S△P2BCBC=S△ABC,确定P2(0,- );
);
试题解析:(1)解:∵一次函数y=-x+b的图象经过点A(-1,4)
∴-(-1)+b=4,
即b=3,
又∵反比例函数 (k≠0)的图象经过点A(-1,4)
(k≠0)的图象经过点A(-1,4)
∴k=xy=(-1)×4=-4;
(2)证明:∵直线l⊥x轴于点E(-4,0)则直线l解析式为x=-4,
∴直线x=-4与一次函数y=-x+3交于点D,则D(-4,7)
直线x=-4与反比例函数y=- 交于点C,
交于点C,
则C(-4,1)
过点A作AF⊥直线l于点F,
∵A(-1,4),C(-4,1),D(-4,7)
∴CD=6,AF=3,DF=3,FC=3
又∵∠AFD=∠AFC=90°,
由勾股定理得:AC=AD=3
又∵AD2+AC2=(3 )2+(3
)2+(3 )2=36
)2=36
CD2=62=36
∴AD2+AC2=CD2
∴由勾股定理逆定理得:△ACD是直角三角形,
又∵AD=AC
∴△ACD是等腰直角三角形;
(3)解:过点A作AP1∥BC,交y轴于P1,则S△PBC=S△ABC
∵B(4,-1),C(-4,1)
∴直线BC的解析式为y=- x
x
∵设直线AP1的解析式为y=- x+b1,把A(-1,4)代入可求b1=
x+b1,把A(-1,4)代入可求b1= ,
,
∴P1(0, ),
),
∴作P1关于x轴的对称点P2,则S△P1BC=S△P2BCBC=S△ABC,
故P2(0,- );即存在P1(0,
);即存在P1(0, ),P2(0,-
),P2(0,- ).
).
考点: 反比例函数综合题


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
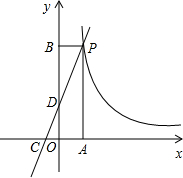 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y=| m |
| x |
| OC |
| OA |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
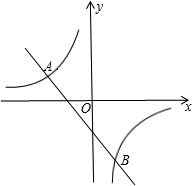 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
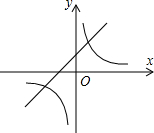 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数y2=
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数y2=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
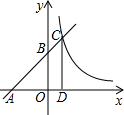 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数y=
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数y=| 4 | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com