Question

小明和几位同学做手的影子游戏时，发现对于同一物体，影子的大小与光源到物体的距离有关.因此，他们认为：可以借助物体的影子长度计算光源到物体的位置.于是，他们做了以下尝试.

（1）如图①，垂直于地面放置的正方形框架ABCD，边长AB为30cm，在其正上方有一灯泡，在灯泡的照射下，正方形框架的横向影子A′B，D′C的长度和为6cm.那么灯泡离地面的高度为           .

（2）不改变①中灯泡的高度，将两个边长为30cm的正方形框架按图②摆放，请计算此时横向影子A′B，D′C的长度和为多少？

（3）有n个边长为a的正方形按图③摆放，测得横向影子A′B，D′C的长度和为b,求灯泡离地面的距离.（写出解题过程，结果用含a,b,n的代数式表示）

 

Answer 1

【答案】

（1）180cm （2）12 cm   (3)

【解析】

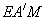试题分析：（1）由题意得A′B=D′C，BM=CM=15；正方形框架ABCD，AB⊥BC，DC⊥BC，AB=CD；所以（SAS），；正方形框架的横向影子A′B，D′C的长度和为6cm，，在直角三角形，；而在直角三角形中，所以，解得h=180cm

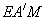（2）不改变①中灯泡的高度，将两个边长为30cm的正方形框架按图②摆放,h=180cm;BM=CM=30cm,AB=CD=30cm;由（1）的证明可得（SAS），，在直角三角形，；而在直角三角形中，所以，解得x=6,所以横向影子A′B，D′C的长度和=2x=12cm

（3）记灯泡为点P，

∵AD∥A′D′，∴∠PAD=∠PA′D′，∠PDA=∠P D′A′．

∴△PAD∽△PA′D′．

根据相似三角形对应高的比等于相似比的性质，可得

设灯泡离地面距离为由题意，得 PM=，PN=AD= ，A′D′= ，

∴

∴

∴

所以x=

考点：全等三角形，三角函数，正方形

点评：本题考查全等三角形，三角函数，正方形，掌握三角形全等的判定方法，熟悉三角函数的定义，掌握正方形的性质是解本题的关键，本题虽是最后一题，但难度不算大