
分析 首先设一片国槐树叶一年的平均滞尘量为x毫克,则一片银杏树叶一年的平均滞尘量为(2x-4)毫克,根据关键语句“若一年滞尘1000毫克所需的银杏树叶的片数与一年滞尘550毫克所需的国槐树叶的片数相同,”可得方程$\frac{1000}{2x-4}$=$\frac{550}{x}$,解方程即可得到答案,注意最后一定要检验.
解答 解:设一片国槐树叶一年的平均滞尘量为x毫克,则一片银杏树叶一年的平均滞尘量为(2x-4)毫克,由题意得:
$\frac{1000}{2x-4}$=$\frac{550}{x}$,
解得:x=22,
经检验:x=22是所列方程的解.
答:一片国槐树叶一年的平均滞尘量为22毫克.
点评 此题主要考查了分式方程的应用,关键是弄清题意,找到题目中的关键语句,列出方程.列分式方程解应用题的一般步骤:设、列、解、验、答.必须严格按照这5步进行做题,规范解题步骤,另外还要注意完整性:如设和答叙述要完整,要写出单位等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这一批灯泡是总体 | B. | 每个灯泡是个体 | ||
| C. | 抽取的10个灯泡是样本 | D. | 抽取的10个灯泡的使用寿命是样本 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
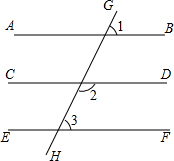 如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°,求证AB∥CD
如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°,求证AB∥CD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com