如果$\frac{2(1-x)}{3}$的值是非负数.则x的取值范围是x≤1．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

10．如果$\frac{2（1-x）}{3}$的值是非负数，则x的取值范围是x≤1．

分析根据题意列出不等式，再根据解不等式得基本步骤求解可得．

解答解：根据题意，得：$\frac{2（1-x）}{3}$≥0，
则2-2x≥0，
-2x≥-2，
∴x≤1，
故答案为：x≤1．

点评本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

20．观察下列各式：
第1个：1×3=3=2²-1
第2个：2×4=8=3²-1
第3个：3×5=15=4²-1
第4个：4×6=24=5²-1
第5个：5×7=35=6²-1
…
这些等式反映出自然数间的某种运算规律．
（1）请你根据规律写出下一个等式：6×8=48=7²-1；
（2）设n（n≥1）表示自然数，请根据这个规律把第n个等式表示出来，并通过你所学过的整式运算知识来验证这个等式成立．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．

如图所示，在四边形ABCD中，AD∥BC，∠A=90°，AB=12，BC=21，AD=16．动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t（秒）．
（1）设△DPQ的面积为S，请用含t的式子表示S；
（2）当t为何值时，PCDQ为平行四边形；
（3）当t为何值时，PD=PQ．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．

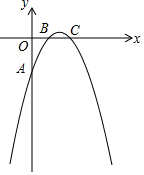已知二次函数y=-x²+ax+b的图象与y轴交于点A（0，-2），与x轴交于点B（1，0）和点C，D（m，0）（m＞2）是x轴上一点．
（1）求二次函数的解析式；
（2）点E是第四象限内的一点，若以点D为直角顶点的Rt△CDE与以A，O，B为顶点的三角形相似，求点E坐标（用含m的代数式表示）；
（3）在（2）的条件下，抛物线上是否存在一点F，使得四边形BCEF为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

5．

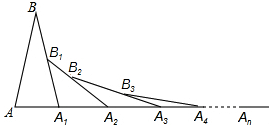如图，已知AB=A₁B，A₁B₁=A₁A₂，A₂B₂=A₂A₃，A₃B₃=A₃A₄…，若∠A=70°，则∠A_n-1A_nB_n-1（n＞2）的度数为（　　）

A．

$\frac{70}{{2}^{n}}$

B．

$\frac{70}{{2}^{n+1}}$

C．

$\frac{70}{{2}^{n-1}}$

D．

$\frac{70}{{2}^{n+2}}$

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．

如图，点A（m，4），B （-4，n）在反比例函数$\frac{k}{x}$（k＞0）的图象上，经过点A、B的直线与x轴相交于点C，与y轴相交于点D
（1）若m=2，完成下列填空
①n=-2，k=8
②将反比例函数y=$\frac{k}{x}$的图象向上平移3个单位长度，所得的图象的函数解析式为y=$\frac{8}{x}$+3
③若正比例函数y=ax（a＞0）与反比例函数y=$\frac{k}{x}$交于点M、N，以MN为斜边作等腰Rt△EMN，则点E所在的图象的函数解析式为y=-$\frac{8}{3}$
（2）连接OA、OB，若tan∠AOD+tan∠BOC=1，求点O到直线AB的距离．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

2．已知x=$\sqrt{5}$-1，则代数式x²-2x-3的值是5-4$\sqrt{5}$．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

19．七年级（1）班买了若干本4元及7元的笔记本作为奖品，共花费40元，则这两种笔记本的数量可能相差（　　）

A．

B．

C．

1或4

D．

不确定