
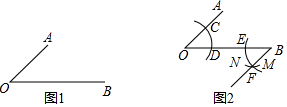 阅读下面材料:数学课上,老师提出如下问题:
阅读下面材料:数学课上,老师提出如下问题:分析 (1)根据作图痕迹知OC=OD=BE=BF,CD=EF,证△OCD≌△BEF得∠FBE=∠AOB,从而得出答案;
(2)根据尺规作图步骤可知.
解答 解:(1)连接CD、EF,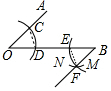
由小明的作图知,
OC=OD=BE=BF,CD=EF,
在△OCD和△BEF中,
∵$\left\{\begin{array}{l}{OC=BE}\\{OD=BF}\\{CD=EF}\end{array}\right.$,
∴△OCD≌△BEF(SSS),
∴∠FBE=∠AOB,
∴小明的作图依据是三边对应相等的两个三角形全等,全等三角形的对应角相等,
故答案为:三边对应相等的两个三角形全等,全等三角形的对应角相等;
(2)他所画的痕迹弧MN是以点E为圆心,CD的长度为半径的弧,
故答案为:E、CD.
点评 本题考查了基本作图和全等三角形的判定与性质;由全等得到角相等是用的全等三角形的性质,熟练掌握三角形全等的性质是正确解答本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
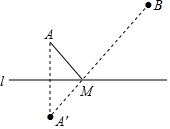 如图,A、B两点在直线l的同侧,在l上求作一点M,使AM+BM最小.小明的做法是:做点A关于直线l的对称点A',连结A'B,交直线l于点M,点M即为所求.请你写出小明这样作图的依据:两点确定一条直线、线段垂直平分线上点到线段两个端点距离相等.
如图,A、B两点在直线l的同侧,在l上求作一点M,使AM+BM最小.小明的做法是:做点A关于直线l的对称点A',连结A'B,交直线l于点M,点M即为所求.请你写出小明这样作图的依据:两点确定一条直线、线段垂直平分线上点到线段两个端点距离相等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将一个边长为a的正方形分割成一个边长为b的小正方形(a>b)和两个梯形,通过两种不同的方法计算阴影部分面积,验证了一个等式,则这个等式是( )
如图,将一个边长为a的正方形分割成一个边长为b的小正方形(a>b)和两个梯形,通过两种不同的方法计算阴影部分面积,验证了一个等式,则这个等式是( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+b)(a-b)=a2-b2 | D. | (a+2b)(a-b)=a2+ab-2b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
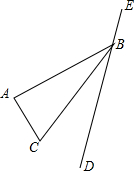 作图题:(画出图形,并写出结论)
作图题:(画出图形,并写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图甲,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形如图乙,通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
如图甲,在边长为a的正方形中挖去一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形如图乙,通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com