
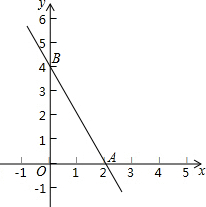 如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.
如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.分析 (1)根据平行一次函数的定义可知:k=-2,再利用待定系数法求出b的值即可;
(2)根据位似比为1:2可知:函数y=kx+b与两坐标的交点坐标,再利用待定系数法求出函数y=kx+b的表达式.
解答  解:(1)由已知得:k=-2,
解:(1)由已知得:k=-2,
把点(3,1)和k=-2代入y=kx+b中得:1=-2×3+b,
∴b=7;
(2)根据位似比为1:2得:函数y=kx+b的图象有两种情况:
①不经过第三象限时,过(1,0)和(0,2),这时表达式为:y=-2x+2;
②不经过第一象限时,过(-1,0)和(0,-2),这时表达式为:y=-2x-2;
点评 本题考查了位似变换和两条直线的平行问题,位似是相似的特殊形式,位似比等于相似比;同时还要熟练掌握若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
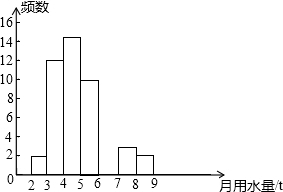 小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 15 | 30% |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
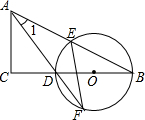 如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com