
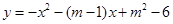 交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.
交x轴负半轴于点A,交y轴正半轴于点B(0,3),顶点C位于第二象限,连结AB,AC,BC.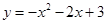 ;(2)
;(2)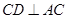 ;(3)S=
;(3)S=
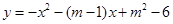 与y轴交于点B(0,3)求得m的值,再由抛物线的顶点在第二象限,即可得到结果;
与y轴交于点B(0,3)求得m的值,再由抛物线的顶点在第二象限,即可得到结果;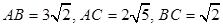 ,根据勾股定理的逆定理可得
,根据勾股定理的逆定理可得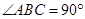 ,再结合∠DCB=∠CAB,即可证得结果;
,再结合∠DCB=∠CAB,即可证得结果;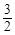 时,如图,EF交AB于点Q,GF交AC于点N,过N做MP//FE交x轴于P点,交BF的延长线点M,BF的延长线交AC于点K,由△AGN∽△KFN根据相似三角形的性质可得
时,如图,EF交AB于点Q,GF交AC于点N,过N做MP//FE交x轴于P点,交BF的延长线点M,BF的延长线交AC于点K,由△AGN∽△KFN根据相似三角形的性质可得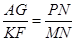 ,即可表示出PN,即可得到结果;当
,即可表示出PN,即可得到结果;当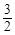 <t≤3时,如图, EF交AB于点N,交AC于点M,BF交AC于点P,由△AME∽△PMF根据相似三角形的性质可得
<t≤3时,如图, EF交AB于点N,交AC于点M,BF交AC于点P,由△AME∽△PMF根据相似三角形的性质可得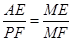 ,即可表示出ME,从而可以求得结果.
,即可表示出ME,从而可以求得结果.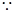 抛物线
抛物线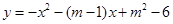 与y轴交于点B(0,3)
与y轴交于点B(0,3)

 抛物线的顶点在第二象限,
抛物线的顶点在第二象限,
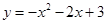 ;
;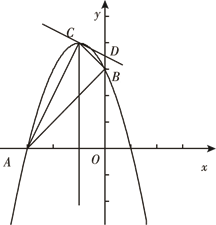
 A(-3,0),B(0,3),C(-1,4)
A(-3,0),B(0,3),C(-1,4)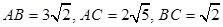
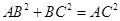
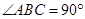
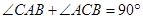
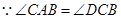
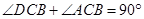
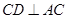 ;
;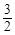 时,如图,EF交AB于点Q,GF交AC于点N,过N做MP//FE交x轴于P点,交BF的延长线点M,BF的延长线交AC于点K
时,如图,EF交AB于点Q,GF交AC于点N,过N做MP//FE交x轴于P点,交BF的延长线点M,BF的延长线交AC于点K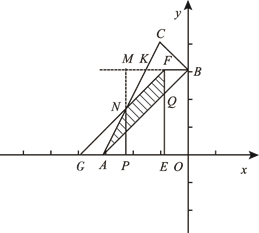
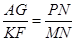
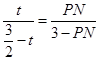
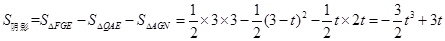
 <t≤3时,如图, EF交AB于点N,交AC于点M,BF交AC于点P
<t≤3时,如图, EF交AB于点N,交AC于点M,BF交AC于点P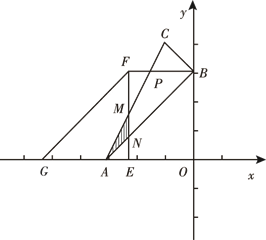
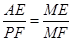
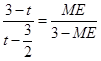
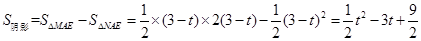



 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源:不详 题型:填空题
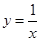 上,点N在直线y=x+3上,设则抛物线y=﹣abx2+(a+b)x的顶点坐标是 .
上,点N在直线y=x+3上,设则抛物线y=﹣abx2+(a+b)x的顶点坐标是 .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
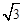 ),且在x轴上截得的线段AB的长为6.
),且在x轴上截得的线段AB的长为6.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
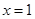 ,它与
,它与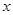 轴交于
轴交于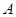 ,
,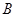 两点,与
两点,与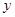 轴交于
轴交于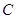 点,点
点,点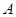 ,
,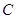 的坐标分别是
的坐标分别是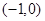 ,
,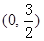 .
.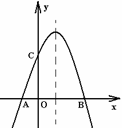
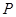 是抛物线上位于
是抛物线上位于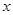 轴上方的一个动点,求△ABP面积的最大值.
轴上方的一个动点,求△ABP面积的最大值.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
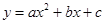 的
的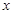 与
与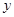 的部分对应值如下表:
的部分对应值如下表: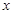 | -7 | -6 | -5 | -4 | -3 | -2 |
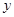 | -27 | -13 | -3 | 3 | 5 | 3 |
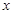 =1时,
=1时,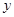 的值为( )
的值为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com