
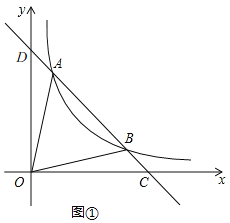
【题目】如图![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() 、
、![]() ,与x轴相交于C点.
,与x轴相交于C点.
![]() 求点A、B的坐标及直线
求点A、B的坐标及直线![]() 的解析式;
的解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 观察第一象限的图象,直接写出不等式
观察第一象限的图象,直接写出不等式![]() 的解集;
的解集;
![]() 如图
如图![]() ,在x轴上是否存在点P,使得
,在x轴上是否存在点P,使得![]() 的和最小?若存在,请说明理由并求出P点坐标.
的和最小?若存在,请说明理由并求出P点坐标.

【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]()
【解析】
(1)先确定出点A,B坐标,再用待定系数法求出直线AB解析式;
(2)先求出点C,D坐标,再用面积的差即可得出结论;
(3)先确定出点P的位置,利用三角形的三边关系,最后用待定系数法求出解析式,即可得出结论.
![]() 点
点![]() 、
、![]() 在双曲线
在双曲线![]() 上,
上,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 点A,B在直线
点A,B在直线![]() 上,
上,
![]() ,
,
![]() ,
,
![]() 直线AB的解析式为
直线AB的解析式为![]() ;
;
![]() 如图
如图![]() ,
,
由![]() 知,直线AB的解析式为
知,直线AB的解析式为![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
![]() 由
由![]() 知,
知,![]() ,
,![]() ,
,
由图象知,不等式![]() 的解集为
的解集为![]() ;
;
![]() 存在,理由:如图2,
存在,理由:如图2,
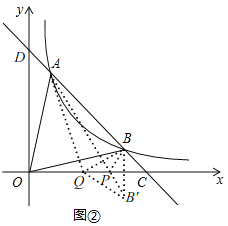
作点![]() 关于x轴的对称点B′(4,-1),连接AB′交x轴于点P,连接BP,在x轴上取一点Q,连接AQ,BQ,
关于x轴的对称点B′(4,-1),连接AB′交x轴于点P,连接BP,在x轴上取一点Q,连接AQ,BQ,
![]() 点B与点B′关于x轴对称,
点B与点B′关于x轴对称,
![]() 点P,Q是BB′的中垂线上的点,
点P,Q是BB′的中垂线上的点,
∴PB′=PB, QB′=QB,
在△AQB′中,AQ+B′Q>AB′
![]() 的最小值为AB′,
的最小值为AB′,
![]() ,B ′(4,-1),
,B ′(4,-1),
![]() 直线AB′的解析式为
直线AB′的解析式为![]() ,
,
令![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
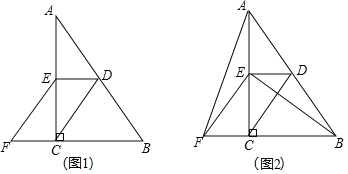
【题目】已知:如图,在![]() 中,
中,![]() ,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且
,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且![]() .
.
![]() 如图1,求证:四边形CDEF是平行四边形;
如图1,求证:四边形CDEF是平行四边形;
![]() 如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与
如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与![]() 面积相等的三角形.
面积相等的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )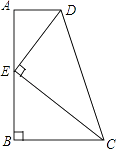
A.CE= ![]() DE
DE
B.CE= ![]() DE
DE
C.CE=3DE
D.CE=2DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地新建的一个企业,每月将生产1960吨污水,为保护环境,该企业计划购置污水处理器,并在如下两个型号种选择:
污水处理器型号 | A型 | B型 |
处理污水能力(吨/月) | 240 | 180 |
已知商家售出的2台A型、3台B型污水处理器的总价为44万元,售出的1台A型、4台B型污水处理器的总价为42万元.
(1)求每台A型、B型污水处理器的价格;
(2)为确保将每月产生的污水全部处理完,该企业决定购买上述的污水处理器,那么他们至少要支付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售.按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:

(1)设装运A种脐橙的车辆数为![]() ,装运B种脐橙的车辆数为
,装运B种脐橙的车辆数为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
①如图1,若BC=4m,则S=m.
②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为m.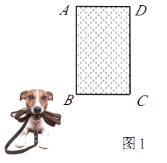
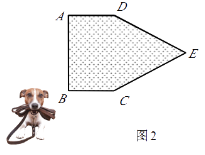
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=﹣ ![]() 的图象与线段AB交于M点,且AM=BM.
的图象与线段AB交于M点,且AM=BM. 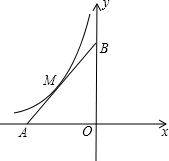
(1)求点M的坐标;
(2)求直线AB的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com