
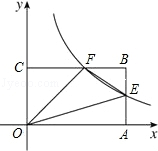
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则:
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则:分析 (1)由S△FOC=3结合反比例函数系数k的几何意义可得出关于k的一元一次方程,解方程即可得出结论;
(2)设点E的坐标为(n,$\frac{6}{n}$),则点B(n,$\frac{12}{n}$),结合个点的特征可得出点F的坐标,由此可用含n的代数式表示出“AB=$\frac{12}{n}$,OA=n,BF=n-$\frac{n}{2}$=$\frac{n}{2}$,BE=$\frac{6}{n}$”,分割矩形OABC利用矩形的、三角形的面积公式即可求出△OEF的面积.
解答 解:(1)∵S△FOC=$\frac{1}{2}$|k|=3,
∴k=±6,
又∵k>0,
∴k=6.
故答案为:6.
(2)设点E的坐标为(n,$\frac{6}{n}$),则点B(n,$\frac{12}{n}$),
令y=$\frac{12}{n}$,则$\frac{12}{n}$=$\frac{6}{x}$,解得:x=$\frac{n}{2}$,
∴点F的坐标为($\frac{n}{2}$,$\frac{12}{n}$).
∴AB=$\frac{12}{n}$,OA=n,BF=n-$\frac{n}{2}$=$\frac{n}{2}$,BE=$\frac{6}{n}$.
S△OEF=S矩形OABC-S△OCF-S△OAE-S△BEF=OA•AB-$\frac{1}{2}$k-$\frac{1}{2}$k-$\frac{1}{2}$BE•BF=$\frac{12}{n}$•n-$\frac{1}{2}$×6-$\frac{1}{2}$×6-$\frac{1}{2}$$\frac{6}{n}$•$\frac{n}{2}$=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查了反比例函数系数k的几何意义、矩形的性质以及三角形的面积公式,解题的关键:(1)得出关于k的方程;(2)设出点E的坐标为(n,$\frac{6}{n}$),用函数n的代数式去表示各线段的长度.本题属于基础题,难度不大,解决该题型题目时,通过分割图形来求面积是关键.


科目:初中数学 来源: 题型:选择题
| A. | 99.55×102 | B. | 9.955×103 | C. | 9.9×103 | D. | 10×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
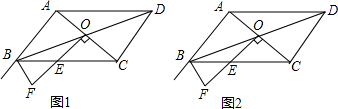
 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
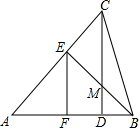 在△ABC中,CD是高,在边AC上有一点E,使EA=EB连接EB交CD于点M.
在△ABC中,CD是高,在边AC上有一点E,使EA=EB连接EB交CD于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com