
【题目】已知直线![]() 或
或![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,
两点,![]() ,则
,则![]() 的值为__________.
的值为__________.
【答案】0或4或-4
【解析】
首先对一次函数进行分类讨论,由于反比例函数![]() 的图象在第一、三象限,所以①
的图象在第一、三象限,所以①![]() 与反比例函数
与反比例函数![]() 交于
交于![]() ,
,![]() 两点,此时根据
两点,此时根据![]() ,以及直线
,以及直线![]() 与坐标轴的夹角为
与坐标轴的夹角为![]() ,可以求出
,可以求出![]() 两点的坐标为
两点的坐标为![]() ,
,![]() ,代入直线
,代入直线![]() 即可解出
即可解出![]() ;②
;②![]() 与反比例函数
与反比例函数![]() 交于
交于![]() ,
,![]() 两点,此时还应再分两种情况,i:
两点,此时还应再分两种情况,i:![]() ,设出
,设出![]() 的横坐标为
的横坐标为![]() ,则纵坐标为
,则纵坐标为![]() ,利用反比例函数的性质列出方程
,利用反比例函数的性质列出方程![]() ,解出
,解出![]() 即可求出
即可求出![]() 的值;ii:
的值;ii:![]() ,和上面同样的方法即可求解;
,和上面同样的方法即可求解;
因为直线![]() 或
或![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,①由于反比例函数
两点,①由于反比例函数![]() 的图象在第一、三象限,当
的图象在第一、三象限,当![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,且
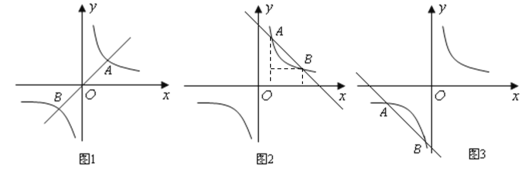
两点,且![]() 时(如图1),因为反比例函数
时(如图1),因为反比例函数![]() 的图象的两支最接近的两点
的图象的两支最接近的两点![]() 与
与![]() 之间的距离为4,此时
之间的距离为4,此时![]() ;②当直线
;②当直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点时,应分两种情况:一是在图2中,
两点时,应分两种情况:一是在图2中,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,则纵坐标为
,则纵坐标为![]() ,则有
,则有![]() ,解得
,解得![]() ,则有
,则有![]() 过点
过点![]() ,代入解析式中可得
,代入解析式中可得![]() ;同理,在图3中,可求得
;同理,在图3中,可求得![]() .
.
故答案是:0或4或-4


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
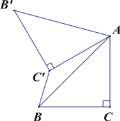
【题目】如图 ,已知△ABC 中,∠C=90°,AC=BC=![]() ,将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
,将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
A.2-![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米.第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为![]() 千米/小时,根据题意可列方程________.
千米/小时,根据题意可列方程________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 延长线上的定点,
延长线上的定点,![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,交射线
,交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
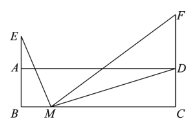
小东根据学习函数的经验,对线段![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小东探究的过程,请补充完整:
(1)对于点![]() 在
在![]() 上的不同位置,画图、测量,得到了线段
上的不同位置,画图、测量,得到了线段![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
| 0.00 | 0.53 | 1.00 | 1.69 | 2.17 | 2.96 | 3.46 | 3.79 | 4.00 |
| 0.00 | 1.00 | 1.74 | 2.49 | 2.69 | 2.21 | 1.14 | 0.00 | 1.00 |
| 4.12 | 3.61 | 3.16 | 2.52 | 2.09 | 1.44 | 1.14 | 1.02 | 1.00 |
在![]() 的长度这三个量中,确定_____的长度是自变量,_____的长度和_____的长度都是这个自变量的函数;
的长度这三个量中,确定_____的长度是自变量,_____的长度和_____的长度都是这个自变量的函数;
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的两个函数的图象;
中,画出(1)中所确定的两个函数的图象;
(3)结合画出的函数图象,解决问题:当![]() 时,
时,![]() 的长度约为________
的长度约为________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
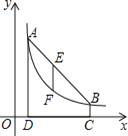
【题目】如图,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的值和反比例函数的解析式;
的值和反比例函数的解析式;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
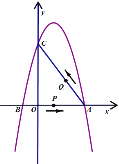
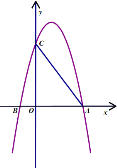
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,已知
,已知![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]()
(1)求抛物线的表达式;
(2)一动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,当点
运动,当点![]() 运动到点
运动到点![]() 时,点
时,点![]() 随之停止运动.设运动时间为
随之停止运动.设运动时间为![]() 秒,当
秒,当![]() 为何值时以
为何值时以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)若点![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 是抛物线上一动点,试判断是否存在以点
是抛物线上一动点,试判断是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形.若存在,请直接写出点
为顶点的四边形是平行四边形.若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
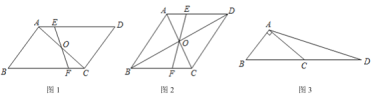
【题目】(1)如图 1,在平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,过点
的中点,过点![]() 的直线分别交
的直线分别交![]() 于点
于点![]() 若平行四边形
若平行四边形![]() 的面积是 8,则四边形
的面积是 8,则四边形![]() 的面积是___________ .
的面积是___________ .
(2)如图 2,在菱形![]() 中,对角线相交于点 O,过点 O 的直线分别交
中,对角线相交于点 O,过点 O 的直线分别交![]() 于点
于点![]() ,若
,若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
(3)如图 3,在![]() 中,
中,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,若
,若![]() ,则
,则![]() 的面积是____________ .
的面积是____________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 价格 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场计划销售这批台灯的总利润至少为1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com