
分析 (1)直接代入点到直线的距离公式计算即可;
(2)计算点Q到直线y=$\sqrt{3}$x+9的距离与半径r对比即可得出结论.
解答 解:(1)因为直线y=x-1,其中k=1,b=-1.
所以点P(1,-1)到直线y=x-1的距离为:
d=$\frac{|k{x}_{0}-{y}_{0}+b|}{\sqrt{1+{k}^{2}}}$=$\frac{|1×1-(-1)+(-1)|}{\sqrt{1+{1}^{2}}}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$;
(2)⊙Q与直线y=$\sqrt{3}$x+9的位置关系为:相切;
理由如下:
圆心Q(0,5)到直线y=$\sqrt{3}$x+9的距离为:d=$\frac{|\sqrt{3}×0-5+9|}{\sqrt{1+(\sqrt{3})^{2}}}$=$\frac{4}{2}$=2,
∵半径r为2,即d=r,
∴⊙Q与直线y=$\sqrt{3}$x+9相切.
点评 本题考查了直线与圆的位置关系、点P到直线y=kx+b的距离公式,也属于阅读材料问题,给定一个新的定义,根据要求运用新的定义解决问题,本题直接运用公式代入计算即可,第二问要与学过的知识相结合,解决问题.


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:解答题
 如图,点P与点Q都在y轴上,且关于x轴对称.
如图,点P与点Q都在y轴上,且关于x轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
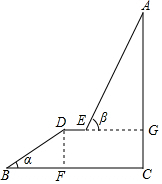 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车达到A处,返程时从A处乘坐升降电梯直接到达C处;已知:AC⊥BC于C,DE∥BC,BC=110米,DE=10米,BD=60米,BD=60米,α=30°,β=60°,求AC的高度.
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车达到A处,返程时从A处乘坐升降电梯直接到达C处;已知:AC⊥BC于C,DE∥BC,BC=110米,DE=10米,BD=60米,BD=60米,α=30°,β=60°,求AC的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com