
”¾ĢāÄæ”æŅŃÖŖµČ±ß”÷ABCŗĶµćP£¬ÉčµćPµ½”÷ABCČż±ßAB”¢AC”¢BCµÄ¾ąĄė·Ö±šĪŖh1£¬h2£¬h3£¬”÷ABCµÄøßĪŖh£®
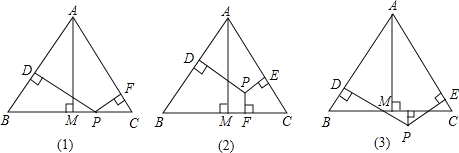
£Ø1£©ČōµćPŌŚŅ»±ßBCÉĻ£¬ČēĶ¼¢Ł£¬“ĖŹ±h3£½0£¬ĒóÖ¤£ŗh1+h2+h3£½h£»
£Ø2£©µ±µćPŌŚ”÷ABCÄŚ£¬ČēĶ¼¢Ś£¬ŅŌ¼°µćPŌŚ”÷ABCĶā£¬ČēĶ¼¢Ū£¬ÕāĮ½ÖÖĒéæöŹ±£¬ÉĻŹö½įĀŪŹĒ·ń³ÉĮ¢£æČō³ÉĮ¢£¬ĒėÓčŅŌÖ¤Ć÷£»Čō²»³ÉĮ¢£¬h1£¬h2£¬h3ÓėhÖ®¼äÓÖÓŠŌõŃłµÄ¹ŲĻµ£¬ĒėĖµ³öÄćµÄ²ĀĻė£¬²¢ĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©¼ū½āĪö£»£Ø2£©µćPŌŚ”÷ABCÄŚŹ±³ÉĮ¢£¬µćPŌŚ”÷ABCĶāŹ±²»³ÉĮ¢£¬ĄķÓɼū½āĪö.
”¾½āĪö”æ
(1)Į¬½ÓAP,½«”÷ABCĆ껿·Ö³É”÷ABPŗĶ”÷APCµÄĆ껿,ĄūÓĆĆ껿¹«Ź½“śČė¼“æÉÖ¤Ć÷.
(2)Į¬½ÓAP”¢BP”¢CP,½«”÷ABCµÄĆ껿·ÖĮŃ³É¼øøöŠ”Čż½ĒŠĪµÄĆ껿֮ŗĶ,“śČėĆ껿¹«Ź½¼ĘĖć¼“æÉ.
£Ø1£©ČēĶ¼1£¬Į¬½ÓAP£¬Ōņ S”÷ABC£½S”÷ABP+S”÷APC
”ą![]() BCAM£½
BCAM£½![]() ABPD+
ABPD+![]() ACPF
ACPF
¼“![]() BCh£½
BCh£½![]() ABh1+
ABh1+![]() ACh2
ACh2
Ó֔ߔ÷ABCŹĒµČ±ßČż½ĒŠĪ
”ąBC£½AB£½AC£¬
”ąh£½h1+h2£»
£Ø2£©µćPŌŚ”÷ABCÄŚŹ±£¬h£½h1+h2+h3£¬ĄķÓÉČēĻĀ£ŗ
ČēĶ¼2£¬Į¬½ÓAP”¢BP”¢CP£¬Ōņ S”÷ABC£½S”÷ABP+S”÷BPC+S”÷ACP
”ą![]() BCAM£½
BCAM£½![]() ABPD+
ABPD+![]() ACPF+
ACPF+![]() BCPE
BCPE
¼“![]() BCh£½
BCh£½![]() ABh1+
ABh1+![]() ACh2+
ACh2+![]() BCh3
BCh3
Ó֔ߔ÷ABCŹĒµČ±ßČż½ĒŠĪ£¬
”ąBC£½AB£½AC£®
”ąh£½h1+h2+h3£»
µćPŌŚ”÷ABCĶāŹ±£¬h£½h1+h2©h3£®
ĄķÓÉČēĻĀ£ŗČēĶ¼3£¬Į¬½ÓPB£¬PC£¬PA
ÓÉČż½ĒŠĪµÄĆ껿¹«Ź½µĆ£ŗS”÷ABC£½S”÷PAB+S”÷PAC©S”÷PBC£¬
¼“![]() BCAM£½
BCAM£½![]() ABPD+
ABPD+![]() ACPE©
ACPE©![]() BCPF£¬
BCPF£¬
”ßAB£½BC£½AC£¬
”ąh1+h2©h3£½h£¬
¼“h1+h2©h3£½h£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼¢Ł£¬Ņ»ĢØµĘ·ÅÖĆŌŚĖ®Ę½×ĄĆęÉĻ£¬µ×׳ABÓėץĆę“¹Ö±£¬µ×׳øßAB£½5cm£¬Į¬øĖBC£½CD£½20cm£¬BC£¬CDÓėABŹ¼ÖÕŌŚĶ¬Ņ»Ę½ĆęÄŚ£®
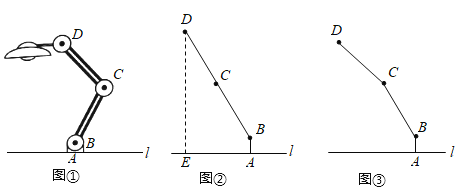
£Ø1£©ČēĶ¼¢Ś£¬×Ŗ¶ÆĮ¬øĖBC£¬CD£¬Ź¹”ĻBCD³ÉĘ½½Ē£¬”ĻABC£½143”ć£¬ĒóĮ¬øĖ¶ĖµćDĄėץĆęlµÄø߶ČDE£®
£Ø2£©½«Ķ¼¢ŚÖŠµÄĮ¬øĖCDŌŁČʵćCÄꏱÕėŠż×Ŗ16”ć£¬ČēĶ¼¢Ū£¬“ĖŹ±Į¬øĖ¶ĖµćDĄėץĆęlµÄøß¶Č¼õŠ”ĮĖ”” ””cm£®
£Ø²Īæ¼Źż¾Ż£ŗsin37”ć£½0.6£¬cos37”ć£½0.8£¬tan37”ć£½0.75£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
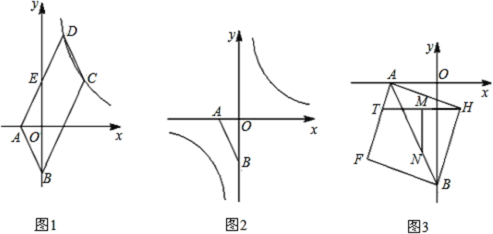
”¾ĢāÄæ”æČēĶ¼1£¬ŅŃÖŖµć![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() ”¢
”¢![]() Āś×ć
Āś×ć![]() £¬
£¬![]() µÄ±ß
µÄ±ß![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £¬ĒŅ
£¬ĒŅ![]() ĪŖ
ĪŖ![]() ÖŠµć£¬Ė«ĒśĻß
ÖŠµć£¬Ė«ĒśĻß![]() ¾¹ż
¾¹ż![]() ”¢
”¢![]() Į½µć£®
Į½µć£®
£Ø1£©Ēó![]() µÄÖµ£»
掙术
£Ø2£©µć![]() ŌŚĖ«ĒśĻß
ŌŚĖ«ĒśĻß![]() ÉĻ£¬µć
ÉĻ£¬µć![]() ŌŚ
ŌŚ![]() ÖįÉĻ£¬ČōŅŌµć
ÖįÉĻ£¬ČōŅŌµć![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬ŹŌĒóĀś×ćŅŖĒóµÄĖłÓŠµć
ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬ŹŌĒóĀś×ćŅŖĒóµÄĖłÓŠµć![]() ”¢
”¢![]() µÄ×ų±ź£»
µÄ×ų±ź£»
£Ø3£©ŅŌĻ߶Ī![]() ĪŖ¶Ō½ĒĻß×÷Õż·½ŠĪ
ĪŖ¶Ō½ĒĻß×÷Õż·½ŠĪ![]() £ØČēĶ¼
£ØČēĶ¼![]() £¬µć
£¬µć![]() ŹĒ±ß
ŹĒ±ß![]() ÉĻŅ»¶Æµć£¬
ÉĻŅ»¶Æµć£¬![]() ŹĒ
ŹĒ![]() µÄÖŠµć£¬
µÄÖŠµć£¬![]() £¬½»
£¬½»![]() ÓŚ
ÓŚ![]() £¬µ±
£¬µ±![]() ŌŚ
ŌŚ![]() ÉĻŌĖ¶ÆŹ±£¬
ÉĻŌĖ¶ÆŹ±£¬![]() µÄÖµŹĒ·ń·¢Éśøıä£æČōøı䣬Ēó³öĘä±ä»Æ·¶Ī§£»Čō²»øı䣬ĒėĒó³öĘäÖµ£¬²¢øų³öÄćµÄÖ¤Ć÷£®
µÄÖµŹĒ·ń·¢Éśøıä£æČōøı䣬Ēó³öĘä±ä»Æ·¶Ī§£»Čō²»øı䣬ĒėĒó³öĘäÖµ£¬²¢øų³öÄćµÄÖ¤Ć÷£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹży£½ax2£«bx£«c(a”Ł0)µÄĶ¼ĻóÓėxÖį½»ÓŚA£¬BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬ĒŅOA£½OC.ŌņĻĀĮŠ½įĀŪ£ŗ¢Łabc£¼0£»¢Ś![]() £¾0£»¢Ūac£b£«1£½0£»¢ÜOA”¤OB£½£
£¾0£»¢Ūac£b£«1£½0£»¢ÜOA”¤OB£½£![]() .ĘäÖŠ½įĀŪÕżČ·µÄŹĒ____________
.ĘäÖŠ½įĀŪÕżČ·µÄŹĒ____________
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ę½ĆęÖ±½Ē×ų±źĻµÄŚ£¬Š”Õż·½ŠĪĶųøńµÄ±ß³¤ĪŖ1øöµ„Ī»³¤¶Č£¬”÷ABCµÄ¶„µćAµÄ×ų±źĪŖ£Ø©3£¬4£©£®
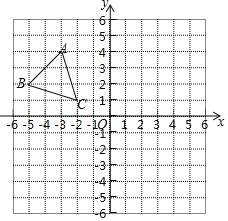
£Ø1£©»³ö”÷ABC¹ŲÓŚyÖįµÄ¶Ō³ĘĶ¼ŠĪ”÷A1B1C1£¬²¢Š“³öA1µÄ×ų±ź£»
£Ø2£©»³ö½«”÷ABCČĘŌµćOÄꏱÕė·½ĻņŠż×Ŗ90”ćµĆµ½µÄ”÷A2B2C2£¬²¢Š“³öA2µÄ×ų±ź£»
£Ø3£©Ēó³ö£Ø2£©ÖŠµćAĖł¾¹żµÄĀ·¾¶µÄ³¤¶Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬Õż·½ŠĪABCDµÄ¶„µć·Ö±šĪŖA£Ø0£¬1£©£¬B£Ø-1£¬0£©£¬C£Ø0£¬-1£©£¬D£Ø1£¬0£©£®¶ŌÓŚĶ¼ŠĪM£¬øų³öČēĻĀ¶ØŅå£ŗPĪŖĶ¼ŠĪMÉĻČĪŅāŅ»µć£¬QĪŖÕż·½ŠĪABCD±ßÉĻČĪŅāŅ»µć£¬Čē¹ūP£¬QĮ½µć¼äµÄ¾ąĄėÓŠ×ī“óÖµ£¬ÄĒĆ“³ĘÕāøö×ī“óÖµĪŖĶ¼ŠĪMµÄ”°Õż·½¾ą”±£¬¼Ē×÷
ÖŠ£¬Õż·½ŠĪABCDµÄ¶„µć·Ö±šĪŖA£Ø0£¬1£©£¬B£Ø-1£¬0£©£¬C£Ø0£¬-1£©£¬D£Ø1£¬0£©£®¶ŌÓŚĶ¼ŠĪM£¬øų³öČēĻĀ¶ØŅå£ŗPĪŖĶ¼ŠĪMÉĻČĪŅāŅ»µć£¬QĪŖÕż·½ŠĪABCD±ßÉĻČĪŅāŅ»µć£¬Čē¹ūP£¬QĮ½µć¼äµÄ¾ąĄėÓŠ×ī“óÖµ£¬ÄĒĆ“³ĘÕāøö×ī“óÖµĪŖĶ¼ŠĪMµÄ”°Õż·½¾ą”±£¬¼Ē×÷![]() £®
£®
£Ø1£©ŅŃÖŖµć![]() £¬
£¬
¢ŁÖ±½ÓŠ“³ö![]() µÄÖµ£»
掙术
¢ŚÖ±Ļß![]() ÓėxÖį½»ÓŚµćF£¬µ±
ÓėxÖį½»ÓŚµćF£¬µ±![]() Č”×īŠ”ÖµŹ±£¬ĒókµÄȔֵ·¶Ī§£»
Č”×īŠ”ÖµŹ±£¬ĒókµÄȔֵ·¶Ī§£»
£Ø2£©![]() µÄŌ²ŠÄĪŖ
µÄŌ²ŠÄĪŖ![]() £¬°ė¾¶ĪŖ1£®Čō
£¬°ė¾¶ĪŖ1£®Čō![]() £¬Ö±½ÓŠ“³ötµÄȔֵ·¶Ī§£®
£¬Ö±½ÓŠ“³ötµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŅ»øö²»ĶøĆ÷µÄŗŠ×Ó֊װӊ“óŠ”ŗĶŠĪדĻąĶ¬µÄ3øöŗģĒņŗĶ2øö°×Ēņ£¬°ŃĖüĆĒ³ä·Ö½ĮŌČ£®
£Ø1£©Ēó“ÓÖŠČĪŅā³éČ”1øöĒņĒ”ŗĆŹĒŗģĒņµÄøÅĀŹ£»
£Ø2£©Ń§Š£¾ö¶ØŌŚ¼×”¢ŅŅĮ½ĆūĶ¬Ń§ÖŠŃ”Č”Ņ»Ćū×÷ĪŖѧɜ“ś±ķ·¢ŃŌ£¬ÖʶØČēĻĀ¹ęŌņ£ŗ“ÓŗŠ×ÓÖŠČĪČ”Į½øöĒņ£¬ČōĮ½ĒņĶ¬É«£¬ŌņŃ”¼×£»ČōĮ½ĒņŅģÉ«£¬ŌņŃ”ŅŅ£¬ÄćČĻĪŖÕāøö¹ęŌņ¹«Ę½Āš£æĒėÓĆĮŠ±ķ·Ø»ņ»Ź÷דĶ¼·Ø¼ÓŅŌĖµĆ÷.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚÖ±½ĒČż½ĒŠĪÖŠ£¬³żÖ±½ĒĶāµÄ5øöŌŖĖŲÖŠ£¬ŅŃÖŖ2øöŌŖĖŲ£ØĘäÖŠÖĮÉŁÓŠ1øöŹĒ±ß£©£¬¾ĶæÉŅŌĒó³öĘäÓąµÄ3øöĪ“ÖŖŌŖĖŲ.¶ŌÓŚČĪŅāČż½ĒŠĪ£¬ĪŅĆĒŠčŅŖÖŖµĄ¼øøöŌŖĖŲ¾ĶæÉŅŌĒó³öĘäÓąµÄĪ“ÖŖŌŖĖŲÄŲ£æĖ¼æ¼²¢½ā“šĻĀĮŠĪŹĢā£ŗ
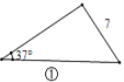

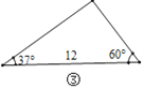
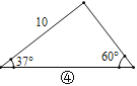
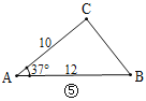
£Ø1£©¹Ū²ģĶ¼¢Ł~Ķ¼¢Ü£¬øł¾ŻĶ¼ÖŠČż½ĒŠĪµÄŅŃÖŖŌŖĖŲ£¬æÉŅŌĒó³öĘäÓąĪ“ÖŖŌŖĖŲµÄŠņŗÅŹĒ____.
£Ø2£©ČēĶ¼¢Ż£¬ŌŚ![]() ÖŠ£¬ŅŃÖŖ
ÖŠ£¬ŅŃÖŖ![]() £¬
£¬![]() £¬
£¬![]() £¬ÄÜ·ńĒó³öBCµÄ³¤¶Č£æČē¹ūÄÜ£¬ĒėĒó³öBCµÄ³¤¶Č£»Čē¹ū²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ.£Ø²Īæ¼Źż¾Ż£ŗ
£¬ÄÜ·ńĒó³öBCµÄ³¤¶Č£æČē¹ūÄÜ£¬ĒėĒó³öBCµÄ³¤¶Č£»Čē¹ū²»ÄÜ£¬ĒėĖµĆ÷ĄķÓÉ.£Ø²Īæ¼Źż¾Ż£ŗ![]() £¬
£¬![]() £¬
£¬![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() ”¢
”¢![]() ·Ö±šŹĒ
·Ö±šŹĒ![]() ”¢
”¢![]() µÄÖŠµć£¬Į¬½Ó
µÄÖŠµć£¬Į¬½Ó![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() £¬ĒŅ
£¬ĒŅ![]() .
.
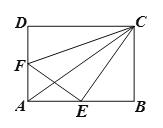
£Ø1£©ĒóÖ¤£ŗ![]() £»
£»
£Ø2£©Čō![]() £¬Ēó
£¬Ēó![]() µÄ³¤£»
µÄ³¤£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Ēó³ö![]() µÄĶā½ÓŌ²Ō²ŠÄÓė
µÄĶā½ÓŌ²Ō²ŠÄÓė![]() µÄĶā½ÓŌ²Ō²ŠÄÖ®¼äµÄ¾ąĄė£æ
µÄĶā½ÓŌ²Ō²ŠÄÖ®¼äµÄ¾ąĄė£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com