
 如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).分析 (1)易证△BAP≌△PQD,从而得到DQ=AP=t,从而可以求出∠PBD的度数和点D的坐标.
(2)延长OA到点F,使得AF=CE,连接BF,利用全等三角形的判定和性质解答即可;
(3)由于∠EBP=45°,故图1是以正方形为背景的一个基本图形,容易得到EP=AP+CE.由于△PBE底边不定,故分三种情况讨论,借助于三角形全等及勾股定理进行求解,然后结合条件进行取舍,最终确定符合要求的t值.
解答 解:(1)如图1,
由题可得:AP=OQ=1×t=t(秒)
∴AO=PQ.
∵四边形OABC是正方形,
∴AO=AB=BC=OC,
∠BAO=∠AOC=∠OCB=∠ABC=90°.
∵DP⊥BP,
∴∠BPD=90°.
∴∠BPA=90°-∠DPQ=∠PDQ.
∵AO=PQ,AO=AB,
∴AB=PQ.
在△BAP和△PQD中,
$\left\{\begin{array}{l}{∠BAP=∠PQD}\\{∠BPA=∠PDQ}\\{AB=PQ}\end{array}\right.$,
∴△BAP≌△PQD(AAS).
∴AP=QD,BP=PD.
∵∠BPD=90°,BP=PD,
∴∠PBD=∠PDB=45°.
∵AP=t,
∴DQ=t.
∴点D坐标为(t,t).
故答案为:45°,(t,t).
(2)延长OA到点F,使得AF=CE,连接BF,如图2所示.
在△FAB和△ECB中,
$\left\{\begin{array}{l}{AB=BC}\\{∠BCE=∠BAF}\\{CE=AF}\end{array}\right.$,
∴△FAB≌△ECB.
∴FB=EB,∠FBA=∠EBC.
∵∠EBP=45°,∠ABC=90°,
∴∠ABP+∠EBC=45°.
∴∠FBP=∠FBA+∠ABP
=∠EBC+∠ABP=45°.
∴∠FBP=∠EBP.
在△FBP与△EBP中,
$\left\{\begin{array}{l}{FB=EB}\\{∠FBP=∠EBP}\\{BP=BP}\end{array}\right.$,
∴△FBP≌△EBP(SAS).
∴FP=EP.
∴EP=FP=FA+AP
=CE+AP.
(3)①若PB=PE,
由△PAB≌△DQP得PB=PD,
显然PB≠PE,
∴这种情况应舍去.
②若EB=EP,
则∠PBE=∠BPE=45°.
∴∠BEP=90°.
∴∠PEO=90°-∠BEC=∠EBC.
在△POE和△ECB中,
$\left\{\begin{array}{l}{∠PEO=∠EBC}\\{∠POE=∠ECB}\\{EP=BE}\end{array}\right.$,
∴△POE≌△ECB(AAS).
∴OE=CB=OC.
∴点E与点C重合(EC=0).
∴点P与点O重合(PO=0).
∵点B(-4,4),
∴AO=CO=4.
此时t=AP=AO=4.
③若BP=BE,
在Rt△BAP和Rt△BCE中,
$\left\{\begin{array}{l}{BA=BC}\\{BP=BE}\end{array}\right.$,
∴Rt△BAP≌Rt△BCE(HL).
∴AP=CE.
∵AP=t,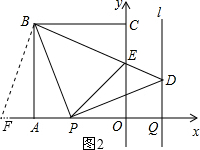
∴CE=t.
∴PO=EO=4-t.
∵∠POE=90°,
∴PE=$\sqrt{P{O}^{2}+E{O}^{2}}$=$\sqrt{2}$(4-t).
延长OA到点F,使得AF=CE,连接BF,如图2所示.
在△FAB和△ECB中,
$\left\{\begin{array}{l}{AB=CB}\\{∠BAF=∠BCE=90°}\\{AF=CE}\end{array}\right.$,
∴△FAB≌△ECB.
∴FB=EB,∠FBA=∠EBC.
∵∠EBP=45°,∠ABC=90°,
∴∠ABP+∠EBC=45°.
∴∠FBP=∠FBA+∠ABP
=∠EBC+∠ABP=45°.
∴∠FBP=∠EBP.
在△FBP和△EBP中,
$\left\{\begin{array}{l}{BF=BE}\\{∠FBP=∠EBP}\\{BP=BP}\end{array}\right.$,
∴△FBP≌△EBP(SAS).
∴FP=EP.
∴EP=FP=FA+AP
=CE+AP.
∴EP=t+t=2t.
∴$\sqrt{2}$(4-t)=2t.
解得:t=4$\sqrt{2}$-4
∴当t为4秒或(4$\sqrt{2}$-4)秒时,△PBE为等腰三角形.
点评 本题考查了正方形的性质、等腰三角形的性质、全等三角形的性质与判定、勾股定理等知识,考查了分类讨论的思想,考查了利用基本活动经验解决问题的能力,综合性非常强.熟悉正方形与一个度数为45°的角组成的基本图形(其中角的顶点与正方形的一个顶点重合,角的两边与正方形的两边分别相交)是解决本题的关键.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
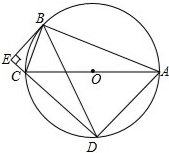 ⊙O是△ABC的外接圆,∠ABC=90°,弦BD=BA,BE是⊙O的切线交DC的延长线于点E.
⊙O是△ABC的外接圆,∠ABC=90°,弦BD=BA,BE是⊙O的切线交DC的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
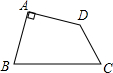 如图,四边形ABCD是一个四边形的草坪,通过测量,获得如下数据:AB=4m,BC=7m,AD=3m,CD=2$\sqrt{6}$m,请你测算这块草坪的面积.(取近似值2.46,结果保留两个有效数字)
如图,四边形ABCD是一个四边形的草坪,通过测量,获得如下数据:AB=4m,BC=7m,AD=3m,CD=2$\sqrt{6}$m,请你测算这块草坪的面积.(取近似值2.46,结果保留两个有效数字)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
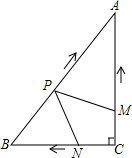 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,动点M,N从但C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN设移动时间为t(单位:秒,0<t<2.5)
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,动点M,N从但C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN设移动时间为t(单位:秒,0<t<2.5)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com