
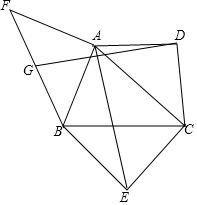
 如图所示,已知△ABC是锐角三角形,以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE,以边AB为直角边向形外作等腰直角三角形ABF,∠BAF=90°,点G为BF的中点,连接GD和AE,试探究GD和AE的数量关系和位置关系,并对你的结论加以证明.
如图所示,已知△ABC是锐角三角形,以边AC、BC为斜边向形外作等腰直角三角形ACD和等腰直角三角形BCE,以边AB为直角边向形外作等腰直角三角形ABF,∠BAF=90°,点G为BF的中点,连接GD和AE,试探究GD和AE的数量关系和位置关系,并对你的结论加以证明. 分析 结论:DG=AE,DG⊥AE.如图,连接FC,分别取CF、BC、BF、AC的中点M、N、G、F,连接GM、MF、DM、EN、AN、FN、DF,右侧MF到H交BC于K,延长EN交DG于O,交GM于J,延长EA交DG于I.只要证明△AFN≌△DFM,△ANE≌DMG,即可解决问题.
解答 解:结论:DG=AE,DG⊥AE.理由如下:
如图,连接FC,分别取CF、BC、BF、AC的中点M、N、G、P,连接GM、MP、DM、EN、AN、PN、DP,延长MP到H交BC于K,延长EN交DG于O,交GM于J,延长EA交DG于I.
由三角形中位线定理可知:PM=$\frac{1}{2}$AF,PN=$\frac{1}{2}$AB,PM∥AF,PN∥AB,
∵AF=AB,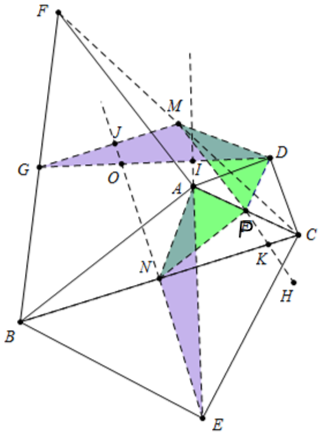
∴PN=PM,
∵∠FAB=90°,
∴∠MPN=90°,
∵DP=AP,∠MPN=∠APD=90°,
∴∠APN=∠MPD,
∴△APN≌△DPM,
∴AN=DM,∠DMP=∠ANP,易证GM=EN,
∵∠GMD=∠GMH+∠DMP=∠NKH+∠ANP=∠PNK+90°+∠ANP=∠PNE+∠ANP=∠ANE,
∴△ANE≌DMG,
∴DG=AE,∠AEN=∠MGD,
∵GM∥BC,EJ⊥BC,
∴EJ⊥GM,
∴∠JGO+∠JOG=90°,
∵∠JOG=∠EOI,
∴∠EOI+∠OEI=90°,
∴∠EIG=90°,
∴DG⊥AE.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质.三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,题目比较难,辅助线比较多.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB,BC延长线于F,E,求证:
如图,在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB,BC延长线于F,E,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
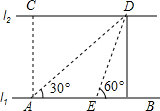 如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.
如图,河的两岸l1与l2互相平行,A、B是l1上的两点,C、D是l2上的两点,某同学在A处测得∠CAB=90°,∠DAB=30°,再沿AB方向走20米到达点E(即AE=20),测得∠DEB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某校把一块三角形的废地ABC改建成一个花园,测得AC=80cm,BC=60cm,AB=100cm.
如图,某校把一块三角形的废地ABC改建成一个花园,测得AC=80cm,BC=60cm,AB=100cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{360}{x}$=$\frac{360}{x-3}$+6 | B. | $\frac{360}{x}$=$\frac{360}{x+3}$+6 | C. | $\frac{360}{x-3}$=$\frac{360}{x}$+6 | D. | $\frac{360}{x+3}$=$\frac{360}{x}$+6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$是无理数 | B. | $\sqrt{8}$的大小介于2和3之间 | ||
| C. | $\sqrt{8}$可以用数轴上的点表示 | D. | $\sqrt{8}$是$\sqrt{2}$的4倍 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com