
【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
(尝试)
(1)当t=2时,抛物线y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的顶点坐标为 ;
(2)判断点A是否在抛物线L上;
(3)求n的值;
(发现)
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
(应用)
二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.

【答案】[尝试](1)(1,﹣2);(2)点A在抛物线L上;(3)n=6;[发现](2,0),(﹣1,6);[应用]不是,理由见解析.
【解析】
[尝试]
(1)将t的值代入“再生二次函数”中,通过配方可得到顶点的坐标;
(2)将点A的坐标代入抛物线L直接进行验证即可;
(3)已知点B在抛物线L上,将该点坐标代入抛物线L的解析式中直接求解,即可得到n的值.
[发现]
将抛物线L展开,然后将含t值的式子整合到一起,令该式子为0(此时无论t取何值都不会对函数值产生影响),即可求出这个定点的坐标.
[应用]
将[发现]中得到的两个定点坐标代入二次函数y=-3x2+5x+2中进行验证即可.
解:[尝试]
(1)∵将t=2代入抛物线L中,得:
y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)=2x2﹣4x=2(x﹣1)2﹣2,
∴此时抛物线的顶点坐标为:(1,﹣2).
(2)∵将x=2代入y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4),得 y=0,
∴点A(2,0)在抛物线L上.
(3)将x=﹣1代入抛物线L的解析式中,得:
n=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)=6.
[发现]
∵将抛物线L的解析式展开,得:
y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)=t(x﹣2)(x+1)﹣2x+4
当x=2时,y=0,当x=-1时,y=6,与t无关,
∴抛物线L必过定点(2,0)、(﹣1,6).
[应用]
将x=2代入y=﹣3x2+5x+2,y=0,即点A在抛物线上.
将x=﹣1代入y=﹣3x2+5x+2,计算得:y=﹣6≠6,
即可得抛物线y=﹣3x2+5x+2不经过点B,
∴二次函数y=﹣3x2+5x+2不是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”.


科目:初中数学 来源: 题型:
【题目】问题:在1~n(n ≥2)这n个自然数中,每次取两个数(不分顺序),使得所取两数之和大于n,共有多少种取法?
探究:不妨设有m种取法,为了探究m与n的关系,我们先从简单情形入手,再逐次递进,最后猜想得出结论.
探究一:在1~2这2个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于2,有多少种取法?
根据题意,有下列取法:1+2,共1种取法.
所以,当n=2时,m=1.
探究二:在1~3这3个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于3,有多少种取法?
根据题意,有下列取法:1+3,2+3,共2种取法.
所以,当n=3时,m=2.
探究三:在1~4这4个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于4,有多少种取法?
根据题意,有下列取法:1+4,2+4,3+4,2+3,共有3+1=4种取法.
所以,当n=4时,m=3+1=4.
探究四:在1~5这5个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于5,有多少种取法?
根据题意,有下列取法:1+5, 2+5, 3+5, 4+5,2+4,3+4,共有4+2=6种不同的取法.
所以,当n=5时,m=4+2=6.
探究五:在1~6这6个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于6,有多少种不同的取法?(仿照上述探究方法,写出解答过程)
探究六:在1~7这7个自然数中,每次取两个不同的数,使得所取的两个数之和大于7,共有 种取法?(直接写出结果)
不妨继续探究n=8,9,···时,m与n的关系.
结论:在1~n这n个自然数中,每次取两个数,使得所取的两个数字之和大于n,当n为偶数时,共有___种取法;当n为奇数时,共有___种取法;(只填最简算式)
应用:(1)各边长都是自然数,最大边长为11的不等边三角形共有 个
(2)各边长都是自然数,最大边长为12的三角形共有 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2﹣5ax+4a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧.
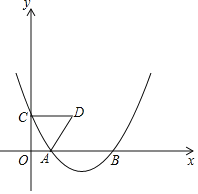
(1)求点A,B的坐标;
(2)当CD∥x轴时,求抛物线的函数表达式;
(3)连接BD,当BD最短时,请直接写出抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为 2000 元,1700 元的A,B两种型号的净水器,下表是近两周的销售情况:
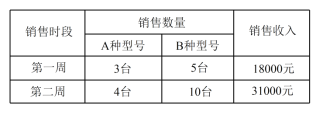
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于 54000 元的金额采购这两种型号的净水器共 30 台,求 A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这 30 台净水器能否实现利润超过12800 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E,延长CA交⊙O于点F.

(1)求证:DE是⊙O切线;
(2)若AB=10cm,DE+EA=6cm,求AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,ABCD的顶点B,C在x轴上,A,D两点分别在反比例函数y=﹣![]() (x<0)与y=
(x<0)与y=![]() (x>0)的图象上,若ABCD的面积为4,则k的值为:_____.
(x>0)的图象上,若ABCD的面积为4,则k的值为:_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为16元的日用品.若按每件23元的价格销售,每月能卖出270件;若按每件28元的价格销售,每月能卖出120件;若规定售价不得低于23元,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数.
(1)试求y与x之间的函数关系式.
(2)在商品不积压且不考虑其他因素的条件下,销售价格定为多少时,才能使每月的毛利润w最大?每月的最大毛利润为多少?
(3)若要使某月的毛利润为1800元,售价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com