
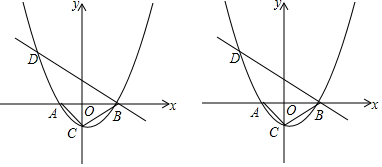
���� ��1�����������A��B���꣬Ȼ�����OA=OC����õ�D���꣬����������y=m��x+1����x-2����mΪ��������m��0������������߽���ʽ��
��2�������⣬����M�˶���·��Ϊ����AF+DF���˶�ʱ�䣺t=AF+$\frac{1}{2}$DF�����ͼ3���������ߣ���AF+$\frac{1}{2}$DFת��ΪAF+FG�����ɴ��߶���̣��õ����߶�AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
��� �⣺
��1��������y=m��x+1����x-2����mΪ��������m��0����x������������ν���A��B���㣬
��y=0�����x=-1��x=2��
��A��-1��0����B��2��0����
��OA=OC��
��C��0��-1����
�ߵ�C��0��-1����������y=m��x+1����x-2���ϣ�
��m����0+1������0-2��=-1��
���m=$\frac{1}{2}$��
�������ߵĺ�������ʽΪ��y=$\frac{1}{2}$��x+1����x-2����
��2���ߡ�DBA=30�㣬
����ֱ��BD�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+b��
��B��2��0����
��0=-$\frac{\sqrt{3}}{3}$��2+b�����b=$\frac{2\sqrt{3}}{3}$��
��ֱ��BD�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$��
����������ʽ�ɵ�$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}x+\frac{2\sqrt{3}}{3}}\\{y=\frac{1}{2}��x+1����x-2��}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=-\frac{2\sqrt{3}+3}{3}}\\{y=\frac{2\sqrt{3}+3}{3}}\end{array}\right.$��
��D��-$\frac{2\sqrt{3}+3}{3}$��$\frac{2\sqrt{3}+3}{3}$����
��ͼ������D��DN��x���ڵ�N������D��DK��x�ᣬ
���KDF=��DBA=30�㣮
����F��FG��DK�ڵ�G����FG=$\frac{1}{2}$DF��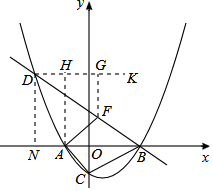
�����⣬����M�˶���·��Ϊ����AF+DF���˶�ʱ�䣺t=AF+$\frac{1}{2}$DF��
��t=AF+FG�����˶���ʱ��ֵ��������AF+FG�ij���ֵ��
�ɴ��߶���̿�֪������AF+FG�ij��ȵ���СֵΪDK��x��֮��Ĵ��߶Σ�
����A��AH��DK�ڵ�H����t��С=AH��AH��ֱ��BD�Ľ��㣬��Ϊ�����F�㣮
��A�������Ϊ-1��ֱ��BD����ʽΪ��y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$��
��y=-$\frac{\sqrt{3}}{3}$����-1��+$\frac{2\sqrt{3}}{3}$=$\sqrt{3}$��
��F��-1��$\sqrt{3}$����
��������������F����Ϊ��-1��$\sqrt{3}$��ʱ����M�������˶���������ʱ���٣�
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ����������ͼ��Ľ��㡢ֱ�������ε����ʡ����߶���̵�֪ʶ���ڣ�1�������C�������ǽ���Ĺؼ����ڣ�2��ȷ��������������F���λ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ر��ǵڣ�2�����ѶȽϴ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����ֱ�ߵ�0cm�̶�����뾶Ϊ5cm����������0���߶��룬������������ֱ�ߵı�Ե�����ع�������ֱ���ϵ�10cm�̶��߶�Ӧ�������ϵĶ���ԼΪ115�㣮�������У�
����ֱ�ߵ�0cm�̶�����뾶Ϊ5cm����������0���߶��룬������������ֱ�ߵı�Ե�����ع�������ֱ���ϵ�10cm�̶��߶�Ӧ�������ϵĶ���ԼΪ115�㣮�������У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���ų��������ӣ���ͨΥ�������Խ��Խ���أ�����������·ij�״����������һ��������ʱ�����ݽ����������ٶ���30-40�����ֵ30�������յ�ֵ40�����õ���Ƶ����Ƶ�������
���ų��������ӣ���ͨΥ�������Խ��Խ���أ�����������·ij�״����������һ��������ʱ�����ݽ����������ٶ���30-40�����ֵ30�������յ�ֵ40�����õ���Ƶ����Ƶ�������| ���ݶ� | Ƶ�� | Ƶ�� |
| 30-40 | 10 | 0.05 |
| 40-50 | 36 | c |
| 50-60 | a | 0.39 |
| 60-70 | b | �� d |
| 70-80 | 20 | 0.10 |
| �ܼ� | 200 | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ÿ��С����ı߳�����1����
��ͼ��ÿ��С����ı߳�����1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
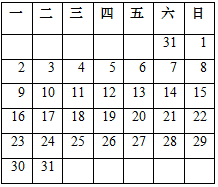 ��ͼ��2017��1�·ݵ�������������������Ȧ��һ�����������ڵ�3�����������Ȧ�����������ĺ�Ϊ63�����������������һ��Ϊ2017��1��28�ţ�
��ͼ��2017��1�·ݵ�������������������Ȧ��һ�����������ڵ�3�����������Ȧ�����������ĺ�Ϊ63�����������������һ��Ϊ2017��1��28�ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4 | B�� | 2 | C�� | 4 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com