
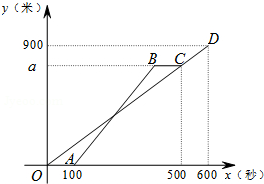
 甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.
甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.分析 (1)根据函数图象可以得到甲跑的路程和甲的速度;
(2)根据函数图象和题意,可以得到乙跑步的速度及乙在途中等候甲的时间;
(3)根据函数图象可以分别求得甲乙的函数关系式,然后联立组成二元一次方程组,即可解答本题.
解答 解:(1)有函数图象可得,
在跑步的全过程中,甲共跑了900米,甲的速度为:900÷600=1.5米/秒,
故答案为:900,1.5;
(2)由图象可得,
甲跑500秒的路程是:500×1.5=750米,
甲跑600米的时间是:(750-150)÷1.5=400秒,
乙跑步的速度是:750÷(400-100)=2.5米/秒,
乙在途中等候甲的时间是:500-400=100秒,
即乙跑步的速度是2.5米/秒,乙在途中等候甲的时间是100秒;
(3)∵D(600,900),A(100,0),B(400,750),
∴OD的函数关系式是y=1.5x,
AB的函数关系式是y=2.5x-250,
根据题意得,$\left\{\begin{array}{l}y=1.5x\\ y=2.5x-250\end{array}\right.$
解得x=250,
250-100=150(秒),
即乙出发150秒时第一次与甲相遇.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
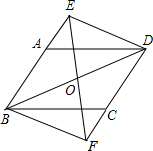 如图,在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交BA、DC的延长线于点E、F,且AE=CF,连接DE、BF.
如图,在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交BA、DC的延长线于点E、F,且AE=CF,连接DE、BF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在正方形ABCD的外侧作直线AP,过点B作BO⊥AP,垂足为O.
在正方形ABCD的外侧作直线AP,过点B作BO⊥AP,垂足为O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com