
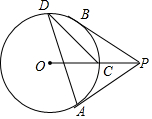
 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )| A. | 26° | B. | 20° | C. | 16° | D. | 30° |
分析 根据四边形的内角和,可得∠BOA,根据等弧所对的圆周角相等,根据圆周角定理,可得答案.
解答 解;如图, 连接OB、OA.
连接OB、OA.
∵PA、PB是⊙O的切线,
∴∠PBO=∠PAO=90°
由四边形的内角和定理,得
∠BOA=360°-90°-90°-76°=104°,
∵∠OPB=∠OPA,∠OPB+∠POB=90°,∠OPA+∠POA=90°,
∴∠POB=∠POA=52°.
∵∠ADC=$\frac{1}{2}$∠AOC=26°,
故选:A.
点评 本题考查了切线的性质、四边形的内角和定理、切线长定理、直角三角形的性质等知识,解题的关键啊灵活运用所学知识解决问题,学会添加常用辅助线,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
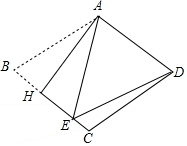 如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )
如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )| A. | 10° | B. | 15° | C. | 18° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如果一条抛物线y=ax2+bx+c(a≠0)与x轴的两个交点为A,B(点A在点B的左侧),顶点为P,连接PA,PB,那么称△PAB为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴的两个交点为A,B(点A在点B的左侧),顶点为P,连接PA,PB,那么称△PAB为这条抛物线的“抛物线三角形”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com