
已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
分析:灵活运用垂直的定义,注意由垂直可得90°角,由90°角可得垂直,结合平行线的判定和性质,只要证得∠ADC=90°,即可得CD⊥AB .
.
证明:∵ DG⊥BC,AC⊥BC(已知),
∴ ∠DGB=∠ACB=90°(垂直定义),
∴ DG∥AC(同位角相等,两直线平行).
∴ ∠2=∠ACD(两直线平行,内错角相等).
∵ ∠1=∠2(已知),
∴ ∠1=∠ACD(等量代换),
∴ EF∥CD(同位角相等,两直线平行).
∴ ∠AEF=∠ADC(两直线平行,同位角相等).
∵ EF⊥AB(已知),∴ ∠AEF=90°(垂直定义),
∴ ∠ADC=90°(等量代换).
∴ CD⊥AB(垂直定义).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
认真阅读下面关于三角形内、外角平分线所夹的 探究片段,完成所提出的问题.
探究片段,完成所提出的问题.
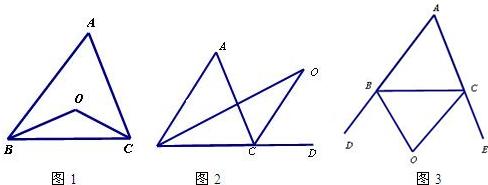
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+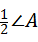 ,理由如下:
,理由如下:
∵ BO和CO分别是∠ABC和∠ACB的角平分线,
∴ .
.
∴ 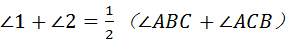 .
.
又∵∠ABC+∠ACB=180°﹣∠A,
∴ 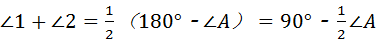 .
.
∴ ∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣ ∠A)
∠A)
=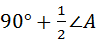 .
.
探究2:如图2中,O是 ∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
结论: .
|
查看答案和解析>>
科目:初中数学 来源: 题型:
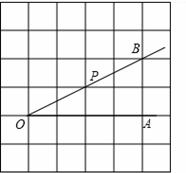
如图,点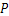 是∠
是∠ 的边
的边 上的一点.
上的一点.
(1)过点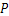 画
画 的垂线,交
的垂线,交 于点
于点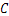 ;
;
(2)过点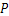 画
画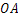 的
的 垂线,垂足为点H;
垂线,垂足为点H;
(3)线段PH的长度是点P到直线________的距离,线段_________的长度是点C到直线OB的距离,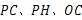 这三条线段的大小关系是__________(用“<”号连接).
这三条线段的大小关系是__________(用“<”号连接).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com