练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．一个正多边形的一个内角是与其相邻的一个外角的3倍，则这个正多边形的边数是8．

    分析 首先设正多边形的一个外角等于x°，由在正多边形中，一个内角的度数恰好等于它相邻的外角的3倍，即可得方程：x+3x=180，解此方程即可求得答案．

    解答 解：设正多边形的一个外角等于x°，
    ∵一个内角的度数恰好等于它相邻的外角的3倍，
    ∴这个正多边形的一个内角为：3x°，
    ∴x+3x=180，
    解得：x=45，
    ∴这个正多边形的边数是：360°÷45°=8．
    故答案为：8．

    点评 此题考查了多边形的内角和与外角和的知识．此题难度不大，方程思想的应用是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

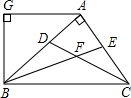    2．如图，AB⊥AC，AG⊥BG，CD、BE分别是∠ACB，∠ABC的角平分线，AG∥BC，下列结论：①∠BAG=2∠ABF；②BA平分∠CBG；③∠ABG=∠ACB；④∠CFB=135°、其中正确的结论是（　　）
    A．①③B．②④C．①③④D．①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．若am=3，an=5，则am+n=15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

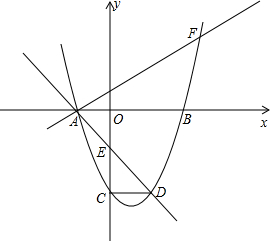    20．如图，在平面直角坐标系中，点O为坐标原点，抛物线y=ax2+bx-5与x轴交于A、B两点（点A在点B的左侧），与y轴交点为C，直线y=-x-2经过点A，交抛物线于点D，交y轴于点E，连接CD，并且∠ADC=45°．
    （1）求抛物线的解析式；
    （2）过点A的直线AF与抛物线的另一个交点为F，sin∠BAF=$\frac{\sqrt{5}}{5}$，求点F的坐标；
    （3）在（2）的条件下，点P是直线AF下方抛物线上一点，过点P作PQ⊥AF垂足为Q，若PE=EQ，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：（-$\frac{5}{3}$）0+|4-$\sqrt{24}$|-$\root{3}{-27}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

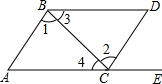    17．如图，点E在AC的延长线上，对于下列给出的四个条件：
    ①∠3=∠4；②∠1=∠2；③∠A=∠DCE；④∠D+∠ABD=180°．
    能判断AB∥CD的有②③④（填正确结论的序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

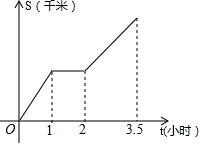    4．星期天，小明从家出发，以15千米/小时的速度骑车去郊游，到达目的地休息一段时间后原路返回，已知小明行驶的路程s（千米）与时间t（小时）之间的函数关系如图所示，则小明返程的速度为（　　）
    A．15千米/小时B．10千米/小时C．6千米/小时D．无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：（$\frac{1}{2}$）-2-6sin30°-（π+2017）0+$\sqrt{9}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：$\sqrt{9}$+（$\sqrt{2}$-1）0-|-3|．

    查看答案和解析>>

    同步练习册答案