
【题目】某天,小王去朋友家借书,在朋友家停留一段时间后,返回家中,如图是他离家的路程 (千米)与时间 (分)关系的图象,根据图象信息,下列说法正确的是 ( )
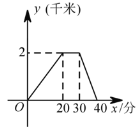
A. 小王去时的速度大于回家的速度 B. 小王去时走上坡路,回家时走下坡路
C. 小王去时所花时间少于回家所花时间 D. 小王在朋友家停留了 ![]() 分
分
【答案】D
【解析】A、根据速度=路程÷时间,可求出小王去时的速度和回家的速度,比较后可得出A不正确;B、题干中未给出路况如何,故B不正确;C、先求出小王回家所用时间,比较后可得出C不正确;D、观察函数图象,求出小王在朋友家停留的时间,故D正确.综上即可得出结论.
A、小王去时的速度为2000÷20=100(米/分),
小王回家的速度为2000÷(40-30)=200(米/分),
∵100<200,
∴小王去时的速度小于回家的速度,A不正确;
B、∵题干中未给出小王去朋友家的路有坡度,
∴B不正确;
C、40-30=10(分),
∵20>10,
∴小王去时所花时间多于回家所花时间,C不正确;
D、∵30-20=10(分),
∴小王在朋友家停留了10分,D正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】向阳花卉基地出售两种花卉——百合和玫瑰,其单价为玫瑰4元/株、百合5元/株,如果同一客户所购的玫瑰数量大于1 200株,那么每株玫瑰还可降价1元.现某鲜花店向向阳花卉基地采购玫瑰1 000~1 500株、百合若干株,恰好花去了9 000元,然后再以玫瑰5元/株、百合6.5元/株的价格卖出.问:此鲜花店应如何采购这两种鲜花才能使获得的毛利润最大?(注:1 000~1 500株,表示大于或等于1 000株,且小于或等于1 500株,毛利润=鲜花店卖出百合和玫瑰所获的总金额—购进百合和玫瑰所需的总金额)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何图形很神奇,由一些多边形组成的图形中离不开边和顶点,它们之间有着很多奥秘等待我们去探索.先看下面一道有趣的关于顶点和边的题:如图所示,图①~图④都是平面图形.

(1)每个图中各有多少个顶点?多少条边?这些边围出多少个区域?请将结果填入下列表格中:

(2)根据(1)中的结论,推断出一个平面图形的顶点数、边数、区域数之间有什么关系(设顶点数为n).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4因式分解的过程.
解:设x2-4x=y,
则原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
解答下列问题:
(1)该同学第二步到第三步运用了因式分解的方法是( )
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果;
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
【答案】(1)C;(2)不彻底,(x-2)4;(3)(x-1)4.
【解析】试题分析:(1)从二步到第三步运用了完全平方和公式;(2)x2-4x+4可运用完全平方差公式因式分解;(3)设x2-2x=y,将(x2-2x)(x2-2x+2)+1变形成y(y+2)+1的形式,再进行因式分解;
试题解析:
(1)运用了C,两数和的完全平方公式;
(2)不彻底;
(x2-4x+4)2=(x-2)4
(3)设x2-2x=y.
(x2-2x)(x2-2x+2)+1
=y(y+2)+1
=y2+2y+1
=(y+1)2…………………………7分
=(x2-2x+1)2
=(x-1)4.
【题型】解答题
【结束】
24
【题目】乘法公式的探究及应用.
探究问题
图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2.

![]()
(1) (2)
(1)图1中长方形纸条的面积可表示为_______(写成多项式乘法的形式).
(2)拼成的图2阴影部分的面积可表示为________(写成两数平方差的形式).
(3)比较两图阴影部分的面积,可以得到乘法公式:____.
结论运用
(4)运用所得的公式计算:
![]() =________;
=________; ![]() =________.
=________.
拓展运用:
(5)计算: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C. 
(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是( )
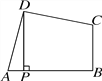
A. 3 B. 2![]() C. 3
C. 3![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.
(1)当x为何值时,OP⊥AP?
(2)求y与x的函数关系式,并写出x的取值范围;
(3)在点P的运动过程中,是否存在x,使△OCM的面积与△ABP的面积之和等于△EMP的面积?若存在,请求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【背景】已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1,d2,d3,且d1=d3=1,d2=2.我们把四个顶点分别在l,m,n,k这四条平行线上的四边形称为“格线四边形” .
【探究1】(1)如图1,正方形ABCD为“格线四边形”,BE⊥l于点E,BE的反向延长线交直线k于点F.求正方形ABCD的边长.
【探究2】(2)如图2,菱形ABCD为“格线四边形”且∠ADC=60°,△AEF是等边三角形,AE⊥k于点E,∠AFD=90°,直线DF分别交直线l,k于点G、点M.求证:EC=DF.
【拓展】(3)如图3,l∥k,等边△ABC的顶点A,B分别落在直线l,k上,AB⊥k于点B,且∠ACD=90°,直线CD分别交直线l、k于点G、点M,点D、点E分别是线段GM、BM上的动点,且始终保持AD=AE,DH⊥l于点H.猜想:DH在什么范围内,BC∥DE?并说明此时BC∥DE的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com