
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B, 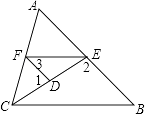
(1)求证:∠AFE=∠ACB;
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
【答案】
(1)证明:∵∠1+∠FDE=180°,∠1,∠2互为补角,
∴∠2=∠FDE,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠B=∠AEF,
∴FE∥BC,
∴∠AFE=∠ACB;
(2)解:∵∠1=80°,∠3=45°,
∴∠FED=80°﹣45°=35°,
∵EF∥BC,
∴∠BCE=∠FED=35°,
∵CE平分∠ACB,
∴∠ACB=2∠BCE=70°,
∴∠AFE=∠ACB=70°.
【解析】(1)求出DF∥AB,推出∠3=∠AEF,求出∠B=∠AEF,得出FE∥BC,根据平行线性质求出即可;(2)求出∠FED=80°﹣45°=35°,根据平行线性质求出∠BCE=∠FED=35°,求出∠ACB=2∠BCE=70°,根据平行线性质求出即可.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】迎接学校“元旦”文艺汇演,八年级某班的全体同学捐款购买了表演道具,经过充分的排练准备,最终获得了一等奖.班长对全体同学的捐款情况绘制成下表:
捐款金额 | 5元 | 10元 | 15元 | 20元 |
捐款人数 | 10人 | 15人 |
| 5人 |
由于填表时不小心把墨水滴在了统计表上,致使表中数据不完整,但知道捐款金额为10元的人数为全班人数的30%,结合上表回答下列问题:
(1)该班共有名同学;
(2)该班同学捐款金额的众数是元,中位数是元.
(3)如果把该班同学的捐款情况绘制成扇形统计图,则捐款金额为20元的人数所对的扇形圆心角为度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,B点坐标为(x、y),且x、y满足|x+y﹣8|+(x﹣y)2=0.
(1)求B点坐标;
(2)如图,点A为y轴正半轴上一点,过点B作BC⊥AB,交x轴正半轴于点C,求证:AB=BC. 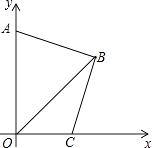
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com