
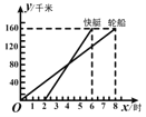
【题目】如图所示,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程y(千米)随时间t(时)变化的图象,根据图象回答下列问题
(1)轮船的行驶速度是___________km/h;
(2)当2≤t≤6时,求快艇行驶过程y与t的函数关系式;
(3)当快艇与乙港相距40 km时,快艇和轮船相距___________km
【答案】(1)20;(2)![]() ;(3)20;
;(3)20;
【解析】
(1)根据速度=路程÷时间即可求得轮船行驶的速度;
(2) 设表示快艇行驶过程的函数式为y=kt+b,根据图象找出点的坐标利用待定系数法即可求出函数解析式;
(3)根据快艇与乙港相距40 km算出轮船行驶的时间,再根据(1)轮船的速度计算出此时轮船行驶的路程,再做减法即可得到答案;
解:(1)从图象可以得到,轮船行驶160千米所需的时间为8小时,
所以轮船的速度为:![]() km/h;
km/h;
故答案为:![]() km/h;
km/h;
(2) 设表示快艇行驶过程的函数式为y=at+b,
根据图象可知,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() ,解得:
,解得:![]() ,
,
故快艇行驶过程y与t的函数关系式为:![]() ;
;
(3)由(2)得到快艇行驶过程y与t的函数关系式为:![]() ,
,
当快艇与乙港相距40 km时,快艇行驶了![]() ㎞,
㎞,
此时得到:![]() ,
,
解得![]() ,
,
由(1)知轮船的行驶速度是20km/h;
根据题意得到:当![]() ,轮船行驶了
,轮船行驶了![]() ,
,
故快艇和轮船相距![]() ;
;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):

(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比产量最少的一天多生产 辆;
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
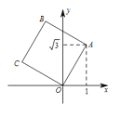
【题目】如图,将正方形OABC放在平面直角坐标系xOy中,O是原点,若点A的坐标为(1,![]() ),则点C的坐标( )
),则点C的坐标( )
A.(-1,![]() )B.(
)B.(![]() )C.
)C.![]() D.(-2,1)
D.(-2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.

请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为__________度,该班共有学生__________人,训练后篮球定时定点投篮平均每个人的进球数是__________.
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
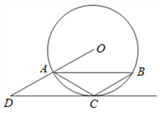
【题目】如图,△ABC内接于⊙O,CA=CB,CD∥AB,CD与OA的延长线交于点D.
(1)求证:CD 是⊙O 的切线;
(2)若∠ACB=120°,OA=2,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
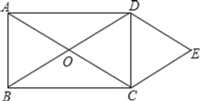
【题目】如图所示,O是矩形ABCD的对角线的交点,作DE//AC,CE//BD,DE、CE相交于点E.
求证:(1)四边形OCED是菱形.
(2)连接OE,若AD=5,CD=3,求菱形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图象法求方程的解,体现了数形结合的方法,它是将方程的解看成两个函数图象交点的横坐标.若关于x的方程x2+a﹣![]() =0(a>0)只有一个整数解,则a的值等于 .
=0(a>0)只有一个整数解,则a的值等于 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com