
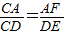 ;
;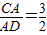 ,圆O1的半径为2,且∠C=30°,求DE的长.
,圆O1的半径为2,且∠C=30°,求DE的长.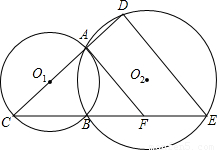
 (1)证明:连接AB.
(1)证明:连接AB. .
. ,
, .
. ,
, .
.

科目:初中数学 来源:2011年湖北省武汉六中中考数学模拟试卷(3月份)(解析版) 题型:选择题
 的自变量x的取值范围是( )
的自变量x的取值范围是( )查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
 时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.
时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《分式》(02)(解析版) 题型:选择题
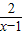 的自变量x的取值范围是( )
的自变量x的取值范围是( )查看答案和解析>>
科目:初中数学 来源:2009年湖北省黄石市中考数学调研试卷(解析版) 题型:选择题
 的自变量x的取值范围是( )
的自变量x的取值范围是( )查看答案和解析>>
科目:初中数学 来源:2004年新疆乌鲁木齐市中考数学试卷(解析版) 题型:解答题
 图象上,若PQ平行于y轴,求出点Q的坐标.
图象上,若PQ平行于y轴,求出点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com