
【题目】在![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转,得到
按逆时针方向旋转,得到![]() .
.
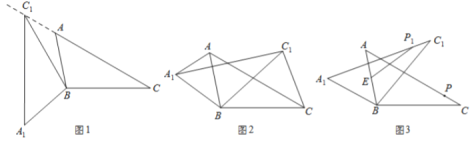
(1)如图 1,当点![]() 在线段
在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
(2)如图 2,连接![]() ,
,![]() .若
.若![]() 的面积为 3,求
的面积为 3,求![]() 的面积;
的面积;
(3)如图 3,点![]() 为线段
为线段![]() 中点,点
中点,点![]() 是线段
是线段![]() 上的动点,在
上的动点,在![]() 绕点
绕点![]() 按逆时针方向旋转的过程中,点
按逆时针方向旋转的过程中,点![]() 的对应点是点
的对应点是点![]() ,求线段
,求线段![]() 长度的最大值与最小值.
长度的最大值与最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)线段
;(3)线段![]() 长度的最大值为8,
长度的最大值为8,![]() 长度的最小值1
长度的最小值1
【解析】
(1)由由旋转的性质可得:![]() ,
,![]() ,又由等腰三角形的性质,即可求得
,又由等腰三角形的性质,即可求得![]() 的度数;
的度数;
(2)由![]() △
△![]() ,易证得
,易证得![]() ,然后利用相似三角形的面积比等于相似比的平方,即可求得
,然后利用相似三角形的面积比等于相似比的平方,即可求得![]() 的面积;
的面积;
(3)由①当![]() 在
在![]() 上运动至垂足点
上运动至垂足点![]() ,
,![]() 绕点
绕点![]() 旋转,使点
旋转,使点![]() 的对应点
的对应点![]() 在线段
在线段![]() 上时,
上时,![]() 最小;②当
最小;②当![]() 在
在![]() 上运动至点
上运动至点![]() ,
,![]() 绕点
绕点![]() 旋转,使点
旋转,使点![]() 的对应点
的对应点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 最大,即可求得线段
最大,即可求得线段![]() 长度的最大值与最小值.
长度的最大值与最小值.
解:(1)如图1,依题意得:△![]() .
.
![]() ,
,![]() .
.
![]() .
.
![]() ;
;
(2)如图2,由(1)知:△![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]()
![]() △
△![]() △
△![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]() ;
;
(3)线段![]() 长度的最大值为8,
长度的最大值为8,![]() 长度的最小值1.
长度的最小值1.
解题过程如下:①如图![]() ,过点
,过点![]() 作
作![]() ,
,![]() 为垂足,
为垂足,
![]() 为锐角三角形,
为锐角三角形,
![]() 点
点![]() 在线段
在线段![]() 上,
上,
在![]() 中,
中,![]() ,
,
当![]() 在
在![]() 上运动,
上运动,![]() 与
与![]() 垂直的时候,
垂直的时候,![]() 绕点
绕点![]() 旋转,使点
旋转,使点![]() 的对应点
的对应点![]() 在线段
在线段![]() 上时,
上时,![]() 最小,最小值为:
最小,最小值为:![]() ;
;
②当![]() 在
在![]() 上运动至点
上运动至点![]() ,
,![]() 绕点
绕点![]() 旋转,使点
旋转,使点![]() 的对应点
的对应点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 最大,最大值为:
最大,最大值为:![]() .
.
综上所述,线段![]() 长度的最大值为8,
长度的最大值为8,![]() 长度的最小值1..
长度的最小值1..




 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() =
=![]() (
(![]() ≠0)图象如图所示,下列结论:①
≠0)图象如图所示,下列结论:①![]() >0;②
>0;②![]() =0;③当
=0;③当![]() ≠1时,
≠1时,![]() >
>![]() ;④
;④![]() >0;⑤若
>0;⑤若![]() =
=![]() ,且
,且![]() ≠
≠![]() ,则
,则![]() =2.其中正确的有( )
=2.其中正确的有( )
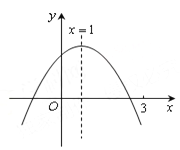
A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间某外地旅行团来重庆的网红景点打卡,游览结束后旅行社对该旅行团做了一次“我最喜爱的巴渝景点”问卷调查(每名游客都填了调査表,且只选了一个景点),統计后发现洪崖洞、长江索道、李子坝轻轨站、磁器口榜上有名.其中选李子坝轻轨站的人数比选磁器口的少![]() 人;选洪崖洞的人数不仅比选磁器口的多,且为整数倍;选磁器口与洪崖洞的人数之和是选李子坝轻轨站与长江索道的人数之和的
人;选洪崖洞的人数不仅比选磁器口的多,且为整数倍;选磁器口与洪崖洞的人数之和是选李子坝轻轨站与长江索道的人数之和的![]() 倍;选长江索道与洪崖洞的人数之和比选李子坝轻轨站与磁器口的人数之和多24人.则该旅行团共有_______人.
倍;选长江索道与洪崖洞的人数之和比选李子坝轻轨站与磁器口的人数之和多24人.则该旅行团共有_______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]() .
.
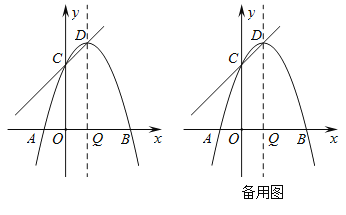
(1)求抛物线的解析式.
(2)若点![]() 是抛物线的对称轴上的一点,以点
是抛物线的对称轴上的一点,以点![]() 为圆心的圆经过
为圆心的圆经过![]() ,
,![]() 两点,且与直线
两点,且与直线![]() 相切,求点
相切,求点![]() 的坐标.
的坐标.
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() 与
与![]() 相似?如果存在,求出点
相似?如果存在,求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),点p为边AB上的一点,![]() CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
CPB=60°,沿CP折叠正方形后,点B落在平面内B’处,B’的坐标为( )
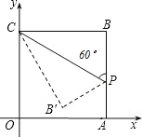
A.(2, 2![]() )B.(
)B.(![]() , 2-2
, 2-2![]() )C.(2, 4-2
)C.(2, 4-2![]() )D.(
)D.(![]() , 4-2
, 4-2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
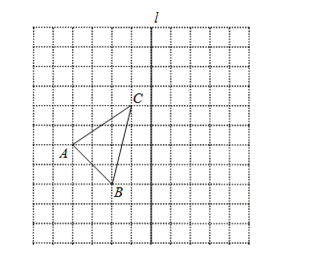
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长都为1,网格中有一个格点
的正方形网格中,每个小正方形的边长都为1,网格中有一个格点![]() (即三角形的顶点都在格点上).
(即三角形的顶点都在格点上).
(1)在图中作出![]() 关于直线l对称的
关于直线l对称的![]() ;(要求A与
;(要求A与![]() ,B与
,B与![]() ,C与
,C与![]() 相对应)
相对应)
(2)作出![]() 绕点C顺时针方向旋转90°后得到的
绕点C顺时针方向旋转90°后得到的![]() ;
;
(3)在(2)的条件下求出线段CB在旋转中所扫过的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注,某市一研究机构为了了解![]() 岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:
岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:
组别 | 年龄段 | 频数(人数) |
第1组 |
| 5 |
第2组 |
|
|
第3组 |
| 35 |
第4组 |
| 20 |
第5组 |
| 15 |
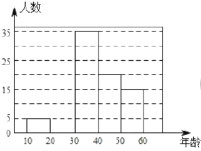
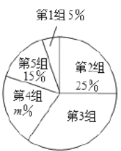
(1)请直接写出![]() 、
、![]() 的值及扇形统计图中第3组所对应的圆心角的度数;
的值及扇形统计图中第3组所对应的圆心角的度数;
(2)请补全上面的频数分布直方图;
(3)假设该市现有![]() 岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少万人?
岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在城市改造中,市政府欲在一条人工河上架一座桥,河的两岸PQ与MN平行,河岸MN上有A、B两个相距50米的凉亭,小亮在河对岸D处测得∠ADP=60°,然后沿河岸走了110米到达C处,测得∠BCP=30°,求这条河的宽.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
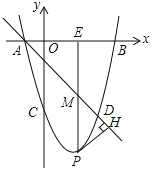
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠OAC=4.
(1)求抛物线的解析式:
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com