
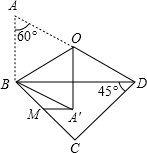
 如图,一副三角板拼在一起,O为AD的中点,AB=a.将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为
如图,一副三角板拼在一起,O为AD的中点,AB=a.将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为| 1 |
| 2 |
| 1 |
| 2 |
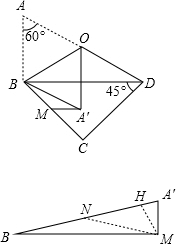 解:由折叠的性质知:AB=A′B=a,∠ABO=∠A′BO;
解:由折叠的性质知:AB=A′B=a,∠ABO=∠A′BO;| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| MN2-MH2 |
| ||
| 4 |
2-
| ||
| 4 |
| A′H2+HM2 |
(
|
| ||||
| 4 |


科目:初中数学 来源: 题型:
如图,一副三角板拼在一起,O为AD的中点,AB=4.将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为____________.

查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省九年级中考数学试卷1(解析版) 题型:填空题
如图,一副三角板拼在一起,O为AD的中点,AB = a.将△ABO沿BO对折于△A′BO,
M为BC上一动点,则A′M的最小值为 .

查看答案和解析>>
科目:初中数学 来源:2011年江苏省宿迁市沭阳县中考一模数学卷 题型:填空题
如图,一副三角板拼在一起,O为AD的中点,AB = a.将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为 .

查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(辽宁沈阳) 题型:填空题
如图,一副三角板拼在一起,O为AD的中点,AB = a.

将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com