
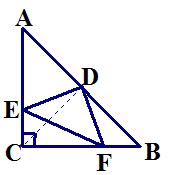
【题目】已知:Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC,CB(或它们的延长线)于E、F,当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证![]() .
.
![]() 当∠EDF绕
当∠EDF绕![]() 点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,![]() 、
、![]() 、
、![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.

【答案】(1)、答案见解析;(2)、![]() -
-![]() =
=![]() .
.
【解析】
试题分析:(1)、首先连接CD,得出△ECD和△FBD全等,根据△CDB的面积等于△ABC面积的一半进行说明;(2)、根据第一题同样的思路得出三角形面积之间的关系.
试题解析:(1)在图2情况下,式子成立.证明如下:
连接CD∵AB=BC,D为AB边的中点 ∴CD⊥AB,∠ACD=∠BCD=45°, ![]()
∵∠ACB=90°,D为AB边的中点 ∴CD=BD=![]() AB ∠B=45°
AB ∠B=45°
∴∠B=∠ACD ∵∠EDC+∠CDF=90°,∠CDF+∠FDB=90° ∴∠EDC=∠FDB
∴△ECD≌△FBD ∴![]()
∵![]() =
=![]() =
=![]()
又![]() ∴
∴![]()
(2)、在图3情况下,式子不成立. 猜想:![]() -
-![]() =
=![]() .
.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】中国古代数学家杨辉的《田亩比类乘除捷法》有这么一道题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何?”意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?经过计算,你的结论是:长比宽多( )
A.12步
B.24步
C.36步
D.48步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P在第三象限,且到x轴的距离为3,到y轴的距离为5,则点P的坐标为( )
A.(3,5)
B.(-5,3)
C.(3,-5)
D.(-5,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. x2﹣4=(x+4)(x﹣4) B. x2﹣2x﹣15=(x+3)(x﹣5)
C. 3mx﹣6my=3m(x﹣6y) D. 2x+4=2(x+4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
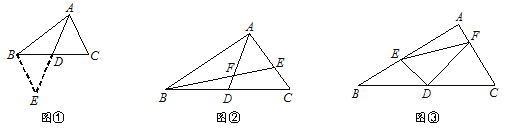
如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
(1)由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
(2)由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=3,EC=2,求线段BF的长.
【灵活运用】
如图③,在△ABC中, ∠A=90°,D为BC中点, DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.试猜想线段BE、CF、EF三者之间的等量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com