
【题目】已知直线BC//ED.
(1)如图1,若点A在直线DE上,且∠B=44°,∠EAC=57°,求∠BAC的度数;
(2)如图2,若点A是直线DE的上方一点,点G在BC的延长线上求证:∠ACG=∠BAC+∠ABC;
(3)如图3,FH平分∠AFE,CH平分∠ACG,且∠FHC比∠A的2倍少60°,直接写出∠A的度数.



【答案】(1)79°;(2)见解析;(3)40°
【解析】分析:(1)由平行线的性质得到∠BAE+∠B=180°,∠EAC=∠C,再由平角的定义即可得到结论;
(2)作AF//BC,得到AF//ED//BC,再由平行线的性质得到∠FAC =∠ACG ,∠ABC=∠FAB,即可得到结论;
(3)作AM//BC,HN//BC, 得到AM//BC//ED,HN//BC//ED,
又设∠ACH=∠GCH=x, ∠AFH=∠EFH =y,则有∠A=2x-2y, ∠FHC=x-y,得到∠A=2∠FHC,又已知∠FHC=2∠A-60°,即可得到结论.
详解:(1)∵BC//ED,∴∠BAE+∠B=180°,∠EAC=∠C,∴∠BAC=180°-∠B-∠EAC=79°;
(2)如图,作AF//BC.又∵BC//ED,∴AF//ED//BC,
∴∠FAC =∠ACG ,且∠ABC=∠FAB,∴∠ACG=∠FAC=∠BAC+∠FAB=∠BAC+∠ABC.
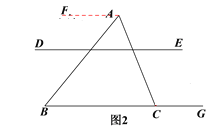
(3)作AM//BC,HN//BC, ∴可证AM//BC//ED,HN//BC//ED,
又设∠ACH=∠GCH=x, ∠AFH=∠EFH =y,
∴∠A=2x-2y, ∠FHC=x-y,
∴∠A=2∠FHC,
又∵∠FHC=2∠A-60°,
∴∠A=40°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(x,y),若点Q的坐标为(x+ay,ax+y)(其中a为常数,且a≠0),则称Q是点P的“a系联动点”.例如:点P(1,2)的“3系联动点”Q的坐标为(7,5).
(1)点(3,0)的“2系联动点”的坐标为 ;若点P的“![]() 系联动点”的坐标是(
系联动点”的坐标是(![]() ,0),则点P的坐标为 ;
,0),则点P的坐标为 ;
(2)若点P(x,y)的“a系联动点”与“![]() 系联动点”均关于x轴对称,则点P分布在 ,请证明这个结论;
系联动点”均关于x轴对称,则点P分布在 ,请证明这个结论;
(3)在(2)的条件下,点P不与原点重合,点P的“a系联动点”为点Q,且PQ的长度为OP长度的3倍,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知
中,已知![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动(点
边上运动(点![]() 不与点
不与点![]() 、
、![]() 重合),且保持
重合),且保持![]() ,连接
,连接![]() 、
、![]() 、
、![]() .在此运动变化的过程中,有下列结论,其中正确的结论是( )
.在此运动变化的过程中,有下列结论,其中正确的结论是( )
①四边形![]() 有可能成为正方形;②
有可能成为正方形;②![]() 是等腰直角三角形;
是等腰直角三角形;
③四边形![]() 的面积是定值;④点
的面积是定值;④点![]() 到线段
到线段![]() 的最大距离为
的最大距离为![]() .
.
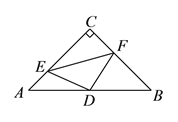
A. ①④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(2m+1)x+m2+m=0.
(1)求证:方程恒有两个不相等的实数根;
(2)设方程两实数根分别为x1,x2,且满足![]() =13,求实数m的值.
=13,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com