
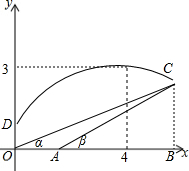
 某防空部队进行射击训练,在地面上设有O、A两个观测点,测得空中固定目标C的仰角分别为α、β,OA=1千米,已知tanα=$\frac{9}{28}$,tanβ=$\frac{3}{8}$.一直升飞机在O点正上方$\frac{5}{3}$千米D点处,向目标C发射防空导弹,导弹飞行的轨道近似为抛物线,当导弹飞行到距O点水平距离4千米时,达到最大高度3千米.建立如图所示的平面直角坐标系.
某防空部队进行射击训练,在地面上设有O、A两个观测点,测得空中固定目标C的仰角分别为α、β,OA=1千米,已知tanα=$\frac{9}{28}$,tanβ=$\frac{3}{8}$.一直升飞机在O点正上方$\frac{5}{3}$千米D点处,向目标C发射防空导弹,导弹飞行的轨道近似为抛物线,当导弹飞行到距O点水平距离4千米时,达到最大高度3千米.建立如图所示的平面直角坐标系.分析 (1)设抛物线为:y=a(x-4)2+3,经过D点,代入解得a;
(2)当x=7时,求得y,然后作比较.
解答 解:(1)由题意可设:CK=9t,OK=28t,AK=24t,则OA=4t,
又∵OA=1千米,则:t=0.25,
∴OK=7,CK=2.25,
即有C的坐标(7,2.25);
设抛物线为:y=a(x-4)2+3,
又∵经过D(0,$\frac{5}{3}$),
∴$\frac{5}{3}$=16a+3,
则:a=-$\frac{1}{12}$,(2分)
∴抛物线为:y=-$\frac{1}{12}$(x-4)2+3;
(2)当x=7时代入解析式有:y=-$\frac{1}{12}$×9+3=2.25,
故该导弹能击中目标C.
点评 本题主要考查二次函数的应用,运用二次函数解决实际问题,比较简单.


科目:初中数学 来源: 题型:填空题
 如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点Bn的坐标为(3×2n-2,$\sqrt{3}$×2n-2).
如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点Bn的坐标为(3×2n-2,$\sqrt{3}$×2n-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
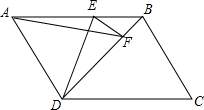 如图,在平行四边形ABCD中,AD⊥BD,点E、点F分别在AB、BD上,且AD=AE=DF,连接DE、AF、EF.
如图,在平行四边形ABCD中,AD⊥BD,点E、点F分别在AB、BD上,且AD=AE=DF,连接DE、AF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
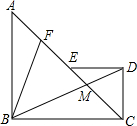 如图,等腰Rt△ABC与等腰RtCDE斜边AC与CE共线,连接BD交AC于M,F为AE中点,连接BF.
如图,等腰Rt△ABC与等腰RtCDE斜边AC与CE共线,连接BD交AC于M,F为AE中点,连接BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com