
 如图,在△ABC中,∠A=70°,AC=BC,以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′BC′,点A恰好落在AC上,连接CC′,求∠ACC′的度数.
如图,在△ABC中,∠A=70°,AC=BC,以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′BC′,点A恰好落在AC上,连接CC′,求∠ACC′的度数. 分析 在△ABC中,可求得∠ABC和∠ACB,在△ABA′中由旋转的性质可求得α的大小,从而可求得∠CBC′,在△BCC′中可求得∠BCC′,从而可求得∠ACC′.
解答 解:
∵AC=BC,
∴∠A=∠ABC=70°,
∴∠ACB=180°-70°-70°=40°,
∵以点B为旋转中心把△ABC按顺时针旋转α度,得到△A′BC′,
∴AB=A′B,BC=BC′,且∠CBC′=α,
∴∠BA′A=∠A=70°,
∴α=40°,
∴∠CBC′=40°,
∴∠BCC′=$\frac{180°-40}{2}$=70°,
∴∠ACC′=∠ACB+∠BCC′=40°+70°=110°.
点评 本题主要考查旋转的性质和等腰三角形的性质,利用旋转的性质和等腰三角形的两底角相等求得α和∠ACB是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | m$<\frac{1}{2}$ | B. | -1$<m<\frac{1}{2}$ | C. | m<-1 | D. | m>-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
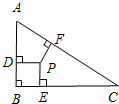 如图,△ABC中,∠B=90°,两直角边AB=3,BC=4,AC=5.三角形内有一点P到各边的距离相等,则这个距离为( )
如图,△ABC中,∠B=90°,两直角边AB=3,BC=4,AC=5.三角形内有一点P到各边的距离相等,则这个距离为( )| A. | 1 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com