
【题目】在一只不透明的袋子中装有1个红色小球,2个黄色小球和若干个黑色小球,这些小球除颜色以外都一样.已知从袋中任意摸出1个红色小球的概率是![]() .
.
(1)袋中黑色小球的数量是 个;
(2)若从袋中随机摸出1个小球,记录好颜色后放回袋中并搅匀,再从袋中任意摸出1个小球,求两次摸出的都是黄色小球的概率是多少?
【答案】(1)1;(2) ![]()
【解析】
(1)根据概率公式求出小球总数,即可得到黑色小球的数量;
(2)首先列举出所求可能发生的情况,然后根据两次摸出的都是黄色小球的结果数,利用概率公式求解即可.
解:(1)设小球总数为n,则![]() ,∴n=4,∴黑色小球的数量是4-1-2=1;
,∴n=4,∴黑色小球的数量是4-1-2=1;
(2)解:将2个黄色小球分别记作“黄1”、“黄2”.从袋中随机摸出1个小球,记录好颜色后放回袋中并搅匀,再从袋中任意摸出1个小球,可能出现的结果有16种,即(红,红),(红,黄1),(红,黄2),(红,黑),(黄1,红),(黄1,黄1),(黄1,黄2),(黄1,黑),(黄2,红),(黄2,黄1),(黄2,黄2),(黄2,黑),(黑,红),(黑,黄1),(黑,黄2),(黑,黑),并且它们出现的可能性相同.其中两次摸出的都是黄色小球(记为事件A)的结果有4种,即(黄1,黄1),(黄1,黄2),(黄2,黄1),(黄2,黄2),所以P(A)=![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
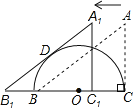
【题目】如图,△ABC中,∠ACB=90°,AB=5,AC=3,BC为半圆O的直径,将△ABC沿射线CB方向平移得到△A1B1C1.当A1B1与半圆O相切于点D时,平移的距离的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3![]() ,求弦AD的长.
,求弦AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D,E分别是△ABC的边AB,AC的中点,H,G是边BC上的点,且HG=![]() BC,S△ABC=24,则图中阴影部分的面积为( )
BC,S△ABC=24,则图中阴影部分的面积为( )

A. 4B. 6C. 8D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】幸福村在推进美丽乡村建设中,决定建设幸福广场,计划铺设相同大小、规格的红色和蓝色地砖,经过调查,获取信息如下表:
类别 | 购买数量低于500块 | 购买数量不低于500块 |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
若购买红色地砖400块,蓝色地砖600块,需付款8600元;若购买红色地砖1000块,蓝色地砖350块,需付款9900元.
(1)红色地砖和蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖1200块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过600块,如何购买付款最少?最少是多少元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
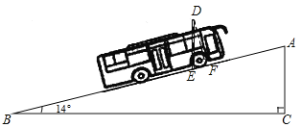
【题目】据城市速递报道,我市一辆高为2.5米的客车,卡在快速路引桥上高为2.55米的限高杆的上端,已知引桥的坡角∠ABC为14°,请结合示意图,用你学过的知识通过数据说明客车不能通过的原因.(参考数据:sin14°=0.24,cos14°=0.97,tan14°=0.25)
查看答案和解析>>
科目:初中数学 来源: 题型:
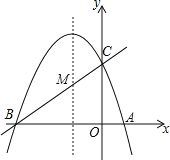
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
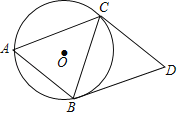
【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=![]() ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
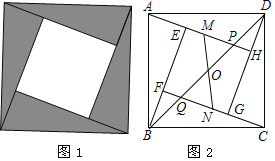
【题目】我国古代数学家赵爽利用弦图证明了勾股定理,这是著名的赵爽弦图(如图1).它是由四个全等的直角三角形拼成了内、外都是正方形的美丽图案.在弦图中(如图2),已知点O为正方形ABCD的对角线BD的中点,对角线BD分别交AH,CF于点P、Q.在正方形EFGH的EH、FG两边上分别取点M,N,且MN经过点O,若MH=3ME,BD=2MN=4![]() .则△APD的面积为_____.
.则△APD的面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com