
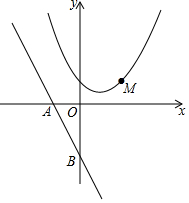
 直线y=-$\frac{4}{3}$x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
直线y=-$\frac{4}{3}$x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).分析 (1)可设点M到直线AB的距离的直线解析式为y=$\frac{3}{4}$x+b,根据待定系数法可求直线解析式,再联立两个直线解析式求得交点坐标,再根据两点间的距离公式即可求解;
(2)可设与直线y=-$\frac{4}{3}$x-4平行的直线解析式为y=-$\frac{4}{3}$x+m,代入抛物线根据判别式得到直线解析式,进一步得到交点坐标,再根据面积公式即可求解.
解答 解:(1)设点M到直线AB的距离的直线解析式为y=$\frac{3}{4}$x+b,则
2=$\frac{3}{4}$×3+b,
解得b=-$\frac{1}{4}$,
∴直线解析式为y=$\frac{3}{4}$x-$\frac{1}{4}$,
联立两个直线解析式可得$\left\{\begin{array}{l}{y=-\frac{4}{3}x-4}\\{y=\frac{3}{4}x-\frac{1}{4}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{9}{5}}\\{y=-\frac{8}{5}}\end{array}\right.$,
则点M到直线AB的距离为$\sqrt{(3+\frac{9}{5})^{2}+(2+\frac{8}{5})^{2}}$=6;
(2)设与直线y=-$\frac{4}{3}$x-4平行的直线解析式为y=-$\frac{4}{3}$x+m,
代入抛物线得x2-4x+5=-$\frac{4}{3}$x+m,即3x2-8x+(15-3m)=0,
△=64-4×3(15-3m)=0,
解得m=$\frac{29}{9}$,
则9x2-24x+16=0,
解得x=$\frac{4}{3}$,
则y=($\frac{4}{3}$)2-4×$\frac{4}{3}$+5=$\frac{13}{9}$,
则交点P的坐标($\frac{4}{3}$,$\frac{13}{9}$),
则△PAB面积的最小值=(3+$\frac{4}{3}$)×(4+$\frac{13}{9}$)-$\frac{1}{2}$×3×4-$\frac{1}{2}$×(3+$\frac{4}{3}$)×$\frac{13}{9}$-$\frac{1}{2}$×$\frac{4}{3}$×(4+$\frac{13}{9}$)=$\frac{325}{6}$.
点评 本题考查了抛物线与x轴的交点,用待定系数法求一次函数的解析式,函数的图象,三角形的面积的应用,能求出一次函数的解析式是解此题的关键,数形结合思想的运用.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com