
分析 (1)因为y=(x-50)w,w=-2x+240,故y与x的关系式为y=-2x2+340x-12000.
(2)用配方法化简函数式求出y的最大值即可.
(3)令y=2250时,求出x的解即可.
解答 解:(1)y=(x-50)•w=(x-50)•(-2x+240)=-2x2+340x-12000,
∴y与x的关系式为:y=-2x2+340x-12000.
(2)y=-2x2+340x-12000=-2(x-85)2+2450
∴当x=85时,y的值最大.
(3)当y=2250时,可得方程-2(x-85)2+2450=2250
解这个方程,得x1=75,x2=95
∴当销售单价为75元或95元时,可获得销售利润2250元.
点评 本题考查的是二次函数的实际应用、一元二次方程的应用等知识,解题的关键是理解题意,学会构建二次函数解决最值问题,会用方程的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的差值 (单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 4 | 2 | -1 | 4 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
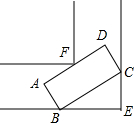 如图所示是一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其矩形平板面ABCD的宽AB为l m,若要想顺利推过 (不可竖起来或侧翻) 直角走廊,平板车的长AD不能超过2.2m.(精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图所示是一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其矩形平板面ABCD的宽AB为l m,若要想顺利推过 (不可竖起来或侧翻) 直角走廊,平板车的长AD不能超过2.2m.(精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即按原路匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.
小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即按原路匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com