
【题目】如图,已知一次函数![]() 的图象与坐标轴分别交于A、B点,AE平分
的图象与坐标轴分别交于A、B点,AE平分![]() ,交
,交![]() 轴于点E.
轴于点E.

(1)直接写出点A和点B的坐标.
(2)求直线AE的表达式.
(3)过点B作BF![]() AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交
AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交![]() 轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
轴于点C,判断四边形ACFD的形状并说明理由,求四边形ACFD的面积.
【答案】(1)A(0,6),B(8,0);(2)y=2x+6;(3)四边形ACFD是菱形,证明见解析;S四边形ACFD=20
【解析】
(1)一次函数![]() ,令x=0求出y值,可得A点坐标,令y=0,求出x值,可得B点坐标,此题得解;
,令x=0求出y值,可得A点坐标,令y=0,求出x值,可得B点坐标,此题得解;
(2)已知A,B点坐标,结合勾股定理可求出AB的长度,再利用角平分线的性质即可求出点E的坐标,根据点A、E的坐标利用待定系数法即可求出直线AE的表达式;
(3)过点B作BF![]() AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交
AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交![]() 轴于点C,连接CD交AF于点G,可得四边形ACFD是平行四边形,证明AD=DF,即可得到四边形ACFD是菱形,证明△AOE∽△BFE,即可得到
轴于点C,连接CD交AF于点G,可得四边形ACFD是平行四边形,证明AD=DF,即可得到四边形ACFD是菱形,证明△AOE∽△BFE,即可得到![]() ,
,![]() ,求得BF和EF,进而求得四边形ACFD的面积.
,求得BF和EF,进而求得四边形ACFD的面积.
(1)∵![]()
当x=0时,y=6
∴A(0,6)
当y=0时,![]()
解得x=8
∴B(8,0)
∴A(0,6),B(8,0)
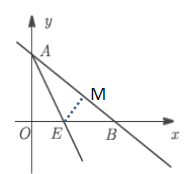
(2)过点E作EM⊥AB于D
∴OA=6,OB=8,
∴AB=![]()
∵AE平分∠BAO,交x轴于点E
∴OE=ME
∴![]()
∴![]()
∴OE=![]() BE
BE
∵OE+BE=OB=8
∴OE=3,BE=5
∴点E的坐标为(3,0)
设直线AE的表达式为y=kx+b
将A(0,6)、E(3,0)代入y=kx+b
![]()
解得:![]()
∴直线AE的表达式为y=2x+6
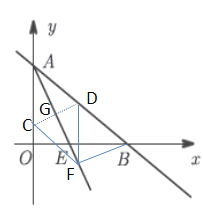
(3)过点B作BF![]() AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交
AE于点F,过点F分别作FD//OA交AB于点D,FC//AB交![]() 轴于点C,连接CD交AF于点G
轴于点C,连接CD交AF于点G
∵FD//OA,FC//AB
∴四边形ACFD是平行四边形
∴∠CAF=∠AFD
∵∠CAF=∠FAD
∴∠AFD=∠FAD
∴AD=DF
∴四边形ACFD是菱形
∵∠AOE=∠BFE=90°,∠AEO=∠BEF
∴△AOE∽△BFE
∴![]()
∵OE=3,OA=6
∴AE=![]()
∴![]()
∴BF=![]()
∵四边形ACFD是菱形
∴DG⊥AF,AG=GF
∴DG=![]() BF=
BF=![]()
∵![]()
∴![]()
∴EF=![]()
∴AF=AE+EF=![]()
S四边形ACFD=AF×DG=![]()
故答案为:四边形ACFD是菱形,证明见解析;S四边形ACFD=20


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销![]() 型号手机四月售价比三月每台降价500元.如果卖出相同数量的
型号手机四月售价比三月每台降价500元.如果卖出相同数量的![]() 型号手机,那么三月销售额为9万元,四月销售额只有8万元.
型号手机,那么三月销售额为9万元,四月销售额只有8万元.
(1)三月![]() 型号手机每台售价为多少元?
型号手机每台售价为多少元?
(2)为了提高利润,该店计划五月购进![]() 型号手机销售,已知
型号手机销售,已知![]() 型号每台进价为3500元,
型号每台进价为3500元,![]() 型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)该店计划六月对![]() 型号的尾货进行销售,决定在四月售价基础上每售出一台
型号的尾货进行销售,决定在四月售价基础上每售出一台![]() 型号手机再返还顾客现金
型号手机再返还顾客现金![]() 元,而
元,而![]() 型号按销售价4400元销售,如要使(2)中所有方案获利相同,
型号按销售价4400元销售,如要使(2)中所有方案获利相同,![]() 应取何值?
应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
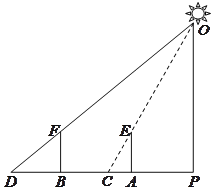
【题目】高高地路灯挂在路边的上方,高傲而明亮,小明拿着一根![]() 米长的竹竿,想量一量路灯的高度,直接量是不可能的,于是,他走到路灯旁的一个地方,竖起竹竿,这时,他量了一下竹竿的影长正好是
米长的竹竿,想量一量路灯的高度,直接量是不可能的,于是,他走到路灯旁的一个地方,竖起竹竿,这时,他量了一下竹竿的影长正好是![]() 米,他沿着影子的方向走,向远处走出两根竹竿的长度(即
米,他沿着影子的方向走,向远处走出两根竹竿的长度(即![]() 米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即
米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即![]() 米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,原来路灯有
米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,原来路灯有![]() 米高呀!”(如图所示)同学们,你觉得小明的判断对吗?
米高呀!”(如图所示)同学们,你觉得小明的判断对吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
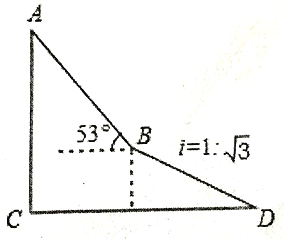
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60![]() 米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l:
米的点D(点D与楼底C在同一水平上)出发,沿斜面坡度为i=l: ![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53![]() ,求楼房AC的高度(参考数据:sin53
,求楼房AC的高度(参考数据:sin53![]() =
=![]() , cos53
, cos53![]() =
=![]() , tan53
, tan53![]() =
=![]() ,
, ![]() ≈1.732,结果精确到0.1米)
≈1.732,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平面直角坐标系内A(2a-1,4),B(-3,3b+1),A、B两点关于y轴对称。
(1)求A、B的坐标
(2)动点P、Q分别从A点、B点同时出发,沿直线AB向右运动,同向而行,P点的速度是每秒2个单位长度,Q点的速度是每秒4个单位长度,设P、Q的运动时间为t秒,当0<t<3时.
①请用含t的代数式表示三角形OPQ的面积S,
②在平面直角坐标系中存在一点M,点M的横纵坐标相等,且满足![]() ,求出点M的坐标,并求出当
,求出点M的坐标,并求出当![]() =15时,三角形OPQ的面积.
=15时,三角形OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36cm,点P从点A开始沿AB边向B点以每秒1cm的速度移动;点Q从点B开始沿BC边向点C以每秒2cm的速度移动,如果点P,Q同时出发,那么过3s时,△BPQ的面积为多少?
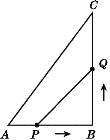
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.
(1)求这种笔和本子的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com