
【题目】如图1,已知抛物线![]() 过点
过点![]() .
.
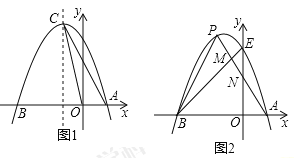
(1)求抛物线的解析式及其顶点C的坐标;
(2)设点D是x轴上一点,当![]() 时,求点D的坐标;
时,求点D的坐标;
(3)如图2.抛物线与y轴交于点E,点P是该抛物线上位于第二象限的点,线段PA交BE于点M,交y轴于点N,![]() 和
和![]() 的面积分别为
的面积分别为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ,顶点C的坐标为-(-1,4);(2)
,顶点C的坐标为-(-1,4);(2)![]() ;(3)
;(3)![]() 的最大值为
的最大值为![]() .
.
【解析】
(1)利用待定系数法,将A,B的坐标代入![]() 即可求得二次函数的解析式;
即可求得二次函数的解析式;
(2)设抛物线对称轴与x轴交于点H,在![]() 中,可求得
中,可求得![]() ,推出
,推出![]() ,可证
,可证![]() ,利用相似三角形的性质可求出AD的长度,进一步可求出点D的坐标,由对称性可直接求出另一种情况;
,利用相似三角形的性质可求出AD的长度,进一步可求出点D的坐标,由对称性可直接求出另一种情况;
(3)设![]() 代入
代入![]() ,求出直线PA的解析式,求出点N的坐标,由
,求出直线PA的解析式,求出点N的坐标,由![]() ,可推出
,可推出![]() ,再用含a的代数式表示出来,最终可用函数的思想来求出其最大值.
,再用含a的代数式表示出来,最终可用函数的思想来求出其最大值.
解:(1)由题意把点![]() 代入
代入![]() ,
,
得,![]() ,
,
解得![]() ,
,
![]()
![]()
∴此抛物线解析式为:![]() ,顶点C的坐标为
,顶点C的坐标为![]()
(2)∵抛物线顶点![]() ,
,
∴抛物线对称轴为直线![]() ,
,
设抛物线对称轴与x轴交于点H,
则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]()
∴当![]() 时,
时,
![]()
如图1,当点D在对称轴左侧时,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
当点D在对称轴右侧时,点D关于直线![]() 的对称点D'的坐标为
的对称点D'的坐标为![]() ,
,
∴点D的坐标为![]() 或
或![]() ;
;
(3)设![]() ,
,
将![]() 代入
代入![]() ,
,
得, ,
,
解得,![]() ,
,
![]()
当![]() 时,
时,![]() ,
,
![]()
如图2,
![]()
![]()
![]()
![]()
![]()
![]() ,
,
由二次函数的性质知,当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
![]() 和
和![]() 的面积分别为m、n,
的面积分别为m、n,
![]() 的最大值为
的最大值为![]() .
.




科目:初中数学 来源: 题型:
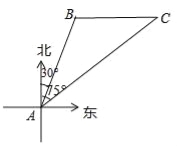
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
![]()
![]() (参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年 3 月 12 日植树节期间, 学校预购进 A、B 两种树苗,若购进 A种树苗 3 棵,B 种树苗 5 棵,需 2100 元,若购进 A 种树苗 4 棵,B 种树苗 10棵,需 3800 元.
(1)求购进 A、B 两种树苗的单价;
(2)若该单位准备用不多于 8000 元的钱购进这两种树苗共 30 棵,求 A 种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
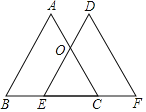
【题目】如图,在△ABC中,AB=AC.将△ABC沿着BC方向平移得到△DEF,其中点E在边BC上,DE与AC相交于点O.连接AE、DC、AD,当点E在什么位置时,四边形AECD为矩形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小李自主创业,开了一家小商品超市.已知超市中某商品的进价为每件20元,售价为每件30元,每个月可卖出180件;如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价必须低于34元,设每件商品的售价上涨![]() 元(
元(![]() 为非负整数),每个月的销售利润为
为非负整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(2)利用函数关系式求出每件商品的售价为多少元时,每个月可获得最大利润?最大利润是多少?
(3)利用函数关系式求出每件商品的售价定为多少元时,每个月的利润恰好是1920元?这时每件商品的利润率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.

(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题]小明在学习时遇到这样一个问题:求不等式x3+3x2﹣x﹣3>0的解集.
他经历了如下思考过程:
[回顾]
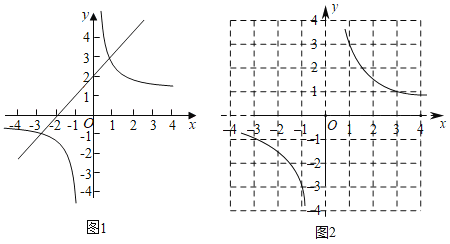
(1)如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=![]() 交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>
交于A (1,3)和B(﹣3,﹣1),则不等式ax+b>![]() 的解集是 .
的解集是 .
[探究]将不等式x3+3x2﹣x﹣3>0按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,不等式两边同除以x并移项转化为x2+3x﹣1>![]() ;
;
当x<0时,不等式两边同除以x并移项转化为x2+3x﹣1<![]() .
.
(2)构造函数,画出图象:
设y3=x2+3x﹣1,y4=![]() ,在同一坐标系中分别画出这两个函数的图象;
,在同一坐标系中分别画出这两个函数的图象;
双曲线y4=![]() 如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
如图2所示,请在此坐标系中画出抛物线y=x2+3x﹣1.(不用列表)
(3)确定两个函数图象公共点的横坐标:
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 .
[解决]
(4)借助图象,写出解集:
结合“探究”中的讨论,观察两个函数的图象可知:不等式x3+3x2﹣x﹣3>0的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
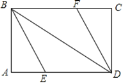
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:△AEB≌△CFD;
(2)当∠ABE= 度时,四边形BEDF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com