
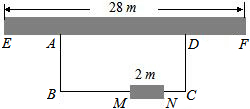
 如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).用砌60米长的墙的材料.
如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).用砌60米长的墙的材料.分析 (1)根据可以砌60m长的墙的材料,即总长度是60m,BC=xm,则AB=$\frac{1}{2}$(60-x+2)m,再根据矩形的面积公式列方程,解一元二次方程即可.
(2)思路同(1),根据实际情况对x的值进行取舍;
(3)利用根的判别式进行判断即可.
解答 解:设矩形花园BC的长为x米,则其宽为$\frac{1}{2}$(60-x+2)米,依题意列方程得:
(1)$\frac{1}{2}$(60-x+2)x=300,
x2-62x+600=0,
解这个方程得:x1=12,x2=50,
∵28<50,
∴x2=50(不合题意,舍去),
∴x=12.
答:当矩形的长BC为12米时,矩形花园的面积为300平方米;
(2)$\frac{1}{2}$(60-x+2)x=480,
x2-62x+960=0,
解这个方程得:x1=32,x2=30,
∵28<30<32,
∴x1=32,x2=30(不合题意,舍去),
答:不能围成480平方米的矩形花园.
(3)$\frac{1}{2}$(60-x+2)x=500,
x2-62x+1000=0,
△=622-4000=-156<0,
则该方程无解,即不能围成500平方米的矩形花园.
答:不能围成500平方米的矩形花园.
点评 本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系求解,注意围墙EF最长可利用28m,舍掉不符合题意的数据.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 问题:求解关于x的一元二次不等式a(x-x1)(x-x2)>0(a≠0,x1<x2)
问题:求解关于x的一元二次不等式a(x-x1)(x-x2)>0(a≠0,x1<x2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
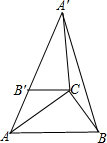 如图.在Rt△ABC中,∠ABC=90°,∠B=60°,BC=2,△A′B′C是由△ABC绕点C顺时针旋转得到的,其中点A′与点A是对应点,点B?与点B是对应点,已知A,B′,A′在同一条直线上.
如图.在Rt△ABC中,∠ABC=90°,∠B=60°,BC=2,△A′B′C是由△ABC绕点C顺时针旋转得到的,其中点A′与点A是对应点,点B?与点B是对应点,已知A,B′,A′在同一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(-21)<+(-21) | B. | -|-10$\frac{1}{2}$|>8$\frac{2}{3}$ | C. | -|-7|=-(-7$\frac{2}{3}$) | D. | -$\frac{5}{6}$<-$\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com