
��֪������y=��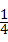 x2+bx+c�ĶԳ���Ϊֱ��x=1������������y�ύ�ڵ�A������ΪB���Գ���BC��x�ύ�ڵ�C����ABC���������1.5.
x2+bx+c�ĶԳ���Ϊֱ��x=1������������y�ύ�ڵ�A������ΪB���Գ���BC��x�ύ�ڵ�C����ABC���������1.5.
��1������������ߵĽ���ʽ,�������A������.
��2�������������Ƿ���ڵ�M��ʹ�á�MAB��������ڡ�ABC�����.������ڣ�������������ĵ�M�����ꣻ��������ڣ���˵�����ɣ�
��3����P���������ϣ�ֱ��PQ��BC��x���ڵ�Q������BQ��
������45��ǵ�ֱ�����ǰ���ͼ2��ʾ���ã����У�һ���������C�غϣ�ֱ�Ƕ���D��BQ�ϣ���һ ������E��PQ��.�������ʱ��Q�������ֱ��BQ�ĺ�������ʽ��
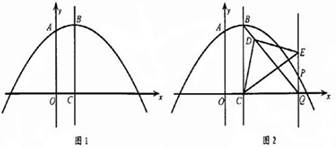
������30��ǵ�ֱ�����ǰ�һ���������C�غϣ�ֱ�Ƕ���D��ֱ��BQ�ϣ���һ������E��PQ�ϣ����P�����꣮
��1��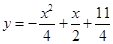 A��0 ��4 ��
A��0 ��4 ��
��2�� 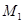 ( ��3, ��1 )
( ��3, ��1 ) 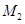 (
4,3/4)
(
4,3/4)
��3����Q��4��0�� ֱ��BQ�Ľ���ʽΪ��y=-x+4��
��P1��1+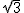 ��
��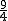 ����P2��1+3
����P2��1+3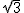 ��-
��-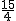 ����P3��1-
����P3��1-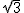 ��
��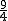 ����
����
P4��1-3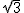 ��-
��-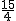 ��
��
����������1���������ߵĶԳ��᷽�̿����b��ֵ��ͨ����ABC��������c��ֵ��������������ߵĽ���ʽ�͵�A�����ꣻ
��2�����������������Ǵ��ڵ�M��ʹ�á�MAB��������ڡ�ABC���������ô����ͬ�������Σ�ֻҪ֤����C��AB�ľ������M��AB�ľ��뼴�ɣ���á�
��3��������������֪��C�ĺ�����Ϊ����B�ĺ����꣬Ȼ������E����PQ���ߵõ���E�ĺ����꣬Ȼ�������ֱ�������εĴ�ֱ��ϵ����֪����Q�����꣬�Ӷ��õ�ֱ��BQ�ķ��̣�ͬ����֪����P�����ꡣ
��3�����ɡ�CDE�ǵ���ֱ�������Σ��ֱ����D��x���PQ�Ĵ��ߣ�ͨ��������ȫ�ȵõ���DQO=45�㣬�����Q�����꣬Ȼ���ô���ϵ�������BQ�Ľ���ʽ��
�ڷֵ�P�ڶԳ���������������ۣ����������������������Q�����꣬Ȼ����������������P�����꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��4 | B��8 | C��-4 | D��16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��1����b+c��ֵ��
��1����b+c��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2012•�����һģ����ͼ����ƽ��ֱ������ϵxOy�У���֪������y=x2+bx+c����A��0��3����B��1��0�����㣬����ΪM��
��2012•�����һģ����ͼ����ƽ��ֱ������ϵxOy�У���֪������y=x2+bx+c����A��0��3����B��1��0�����㣬����ΪM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com