
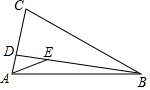
 在△ABC中,AB=BC,∠ABC=30°,D为AC边上一点,连接BD,在BD上取点E,连接AE,若∠AED=30°,DE=2,△BDC的面积为12,则线段BE的长度为6.
在△ABC中,AB=BC,∠ABC=30°,D为AC边上一点,连接BD,在BD上取点E,连接AE,若∠AED=30°,DE=2,△BDC的面积为12,则线段BE的长度为6. 分析 先运用旋转变换,得到△ABE≌△CBF,根据CF∥BD即可得出S△BCD=$\frac{1}{2}$BD×FH=12,设FH=x,则BF=BE=2x,BD=2x+2,进而得到方程$\frac{1}{2}$(2x+2)×x=12,求得x=3,即可得到BE=2x=6.
解答 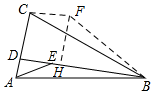 解:如图,将△ABE绕着点B顺时针旋转30°,使得点A与点C重合,得到△BCF,
解:如图,将△ABE绕着点B顺时针旋转30°,使得点A与点C重合,得到△BCF,
过F作FH⊥BD于H,连接CF,则△ABE≌△CBF,
∵∠ABC=30°,∠AED=30°,
∴∠FBH=30°,∠BFC=∠BEA=150°,
∴BF=BE=2FH,∠BFC+∠DBF=180°,
∴CF∥BD,
∴S△BCD=$\frac{1}{2}$BD×FH=12,
设FH=x,则BF=BE=2x,BD=2x+2,
∴$\frac{1}{2}$(2x+2)×x=12,
解得x1=3,x2=-4(舍去)
∴BE=2x=6,
故答案为:6.
点评 本题主要考查了含30°角的直角三角形的性质,等腰三角形的性质以及旋转的性质的综合应用,解决问题的关键是作辅助线构造全等三角形以及含30°角的直角三角形的性质,利用三角形的面积列方程求解.


科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠C=50°,∠B=25°,AD是角平分线,点E在AB上,AE=AC.
如图,△ABC中,∠C=50°,∠B=25°,AD是角平分线,点E在AB上,AE=AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若x1、x2是3x2+4x-5=0的两根,则x1+x2=-$\frac{5}{3}$. | |
| B. | 单项式-$\frac{4{x}^{2}{y}^{2}}{7}$的系数是-4 | |
| C. | 若|x-1|+(y-3)2=0,则x=1,y=3 | |
| D. | 若分式方程$\frac{x}{x-3}$-2=$\frac{{m}^{2}}{x-3}$产生增根则m=3. |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-a)2•a2=-a4 | B. | (-x-2y)(x+2y)=x2-4y2 | ||
| C. | (-3x3y)2=9x9y2 | D. | 2x2y+3yx2=5x2y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全市高三年级学生的睡眠质量 | |
| B. | 了解我校同学对国家设立雄安新区的看法 | |
| C. | 对端午出游旅客上飞机前的安全检查 | |
| D. | 对电影“摔跤吧,爸爸”收视率的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
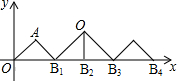 如图:在直角坐标系中,等腰直角三角形OAB的直角边为3厘米,三角形绕B1点旋转,A点落在B2点上,再绕B2点旋转,O点落在B3点上,如此下去,B2017的坐标为(4032+2019$\sqrt{3}$,0).
如图:在直角坐标系中,等腰直角三角形OAB的直角边为3厘米,三角形绕B1点旋转,A点落在B2点上,再绕B2点旋转,O点落在B3点上,如此下去,B2017的坐标为(4032+2019$\sqrt{3}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com