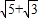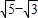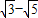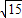观察下列等式12×231=132×21
13×341=143×31
23×352=253×32
34×473=374×43
62×286=682×26
…
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同的规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反应的规律填空,使式子称为“数字对称等式”.
①52×
275
275
=
572
572
×25
②
63
63
×396=693×
36
36
(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9则等式右边的两位数可表示为
10b+a
10b+a
,等式右边的三位数可表示为
100a+10(a+b)+b
100a+10(a+b)+b
;
(3)在(2)的条件下,若a-b=5,等式左右两边的两个三位数的差;
(4)等式左边的两位数与三位数的积能否为2012?若能,请求出左边的两位数;若不能,请说明理由.

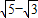 的积为有理数的是( )
的积为有理数的是( )