
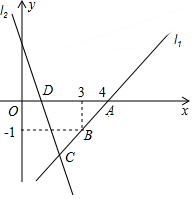
 如图所示,直线l1 经过A,B两点,直线l2的表达式为y=-2x+2,且与x轴交于点D,两直线相交于点C.
如图所示,直线l1 经过A,B两点,直线l2的表达式为y=-2x+2,且与x轴交于点D,两直线相交于点C.分析 (1)设直线l1的表达式为y=kx+b,将A(4,0),B(3,-1)代入得k,b,可得一次函数的解析式;
(2)令y=0,代入直线l2的表达式为y=-2x+2,可得D点坐标,根据两直线相交可得C点坐标,由三角形的面积公式可得结果;
(3)根据△ADP与△ADC的面积相等可得点P的纵坐标,在代入直线l1的表达式可得点P的横坐标,可得点P的坐标.
解答 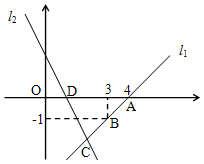 解:(1)设直线l1的表达式为y=kx+b,将A(4,0),B(3,-1)代入得,
解:(1)设直线l1的表达式为y=kx+b,将A(4,0),B(3,-1)代入得,
$\left\{\begin{array}{l}4k+b=0\\ 3k+b=-1\end{array}\right.$
解得 $\left\{\begin{array}{l}k=1\\ b=-4\end{array}\right.$
∴直线l1的表达式为y=x-4;
(2)当y=0时,-2x+2=0
∴x=1
∴D(1,0)
解方程组$\left\{\begin{array}{l}y=x-4\\ y=-2x+2\end{array}\right.$
得 $\left\{\begin{array}{l}x=2\\ y=-2\end{array}\right.$
∴C(2,-2)
∴${S_{△ADC}}=\frac{1}{2}×(4-1)×2=3$
(3)∵△ADP与△ADC的面积相等,
∴设P点的纵坐标为yP,
∴S△ADP=$\frac{1}{2}$×(4-1)×|yP|=3,
解得yP=±2,
∵C点纵坐标为-2,
∴P点纵坐标为2,
∴2=x-4
∴x=6,
∴P点的坐标为(6,2).
点评 此题主要考查了一次函数的综合应用以及待定系数法求一次函数解析式,根据已知结合图形得出点P的纵坐标与点C的纵坐标的绝对值相等是解题关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-2)(x2+1) | B. | (x-2)(x2-1) | C. | (x-2)(x+1)(x-1) | D. | (x-2)(1+x)(1-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
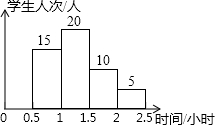 某校为了解学生课业负担的情况,随机抽取了50名七年级学生,调查学生每天完成课外作业所需的平均时间,并绘制了如图所示的频数分布直方图,根据图中信息,完成课外作业所需时间在1.5-2小时的频数是( )
某校为了解学生课业负担的情况,随机抽取了50名七年级学生,调查学生每天完成课外作业所需的平均时间,并绘制了如图所示的频数分布直方图,根据图中信息,完成课外作业所需时间在1.5-2小时的频数是( )| A. | 15 | B. | 20 | C. | 10 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com