
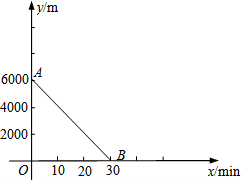
 某日,小敏、小君两人约好去奥体中心打球.小敏13:00从家出发,匀速骑自行车前往奥体中心,小君13:05从离奥体中心6000m的家中匀速骑自行车出发.已知小君骑车的速度是小敏骑车速度的1.5倍.设小敏出发x min后,到达离奥体中心y m的地方,图中线段AB表示y与x之间的函数关系.
某日,小敏、小君两人约好去奥体中心打球.小敏13:00从家出发,匀速骑自行车前往奥体中心,小君13:05从离奥体中心6000m的家中匀速骑自行车出发.已知小君骑车的速度是小敏骑车速度的1.5倍.设小敏出发x min后,到达离奥体中心y m的地方,图中线段AB表示y与x之间的函数关系.分析 (1)根据函数图象可得,小敏家离奥体中心的距离为6000米,她所用时间为30分钟,根据速度=路程÷时间,即可解答;
(2)利用待定系数法,即可求函数解析式;
(3)小君骑车的速度是200×1.5=300(米/分钟),设小君骑自行车时与奥体中心的距离为y1 m,则y1=-300(x-5)+6000,当y1=0时,x=25.30-25=5.即小君先到达奥体中心,小君要等小敏5分钟.
解答 解:(1)小敏家离奥体中心的距离为6000米,她骑自行车的速度为:6000÷30=200(米/分钟).
故答案为:6000,200;
(2)设AB所在直线的函数表达式为y=kx+b,
将点A(0,6000),B(30,0)代入y=kx+b得:
$\left\{\begin{array}{l}b=6000\\ 30k+b=6\end{array}$,
解得 $\left\{\begin{array}{l}b=6000\\ k=-200\end{array}$.
∴AB所在直线的函数表达式为y=-200x+6000.
(3)∵小君骑车的速度是小敏骑车速度的1.5倍.
∴小君骑车的速度是200×1.5=300(米/分钟),
设小君骑自行车时与奥体中心的距离为y1 m,
则y1=-300(x-5)+6000,
当y1=0时,x=25.
30-25=5.
∴小君先到达奥体中心,小君要等小敏5分钟.
点评 本题考查了一次函数的应用,利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
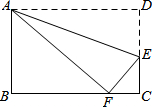 如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,若AB:AD=2:3,则tan∠AFB值是$\frac{2\sqrt{5}}{5}$.
如图,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,若AB:AD=2:3,则tan∠AFB值是$\frac{2\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
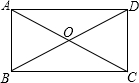 如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠AOD=120°,则AD的长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,AB=3,∠AOD=120°,则AD的长为( )| A. | 3 | B. | 3$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
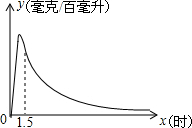 实验数据显示:一般成人喝半斤低度白酒后,其血液中酒精含量y(毫克/百毫升)与时间x(小时)的关系为:当0≤x≤1.5时,y与x成二次函数关系,即y=-200x2+400x;当x≥1.5时,y与x成反比例函数关系,即y=$\frac{k}{x}$.
实验数据显示:一般成人喝半斤低度白酒后,其血液中酒精含量y(毫克/百毫升)与时间x(小时)的关系为:当0≤x≤1.5时,y与x成二次函数关系,即y=-200x2+400x;当x≥1.5时,y与x成反比例函数关系,即y=$\frac{k}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
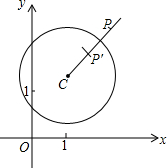 在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com