
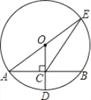
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A. 2![]() B. 8 C. 2
B. 8 C. 2![]() D. 2
D. 2![]()
【答案】D
【解析】连结BE,设⊙O的半径为R,由OD⊥AB,根据垂径定理得AC=BC=![]() AB=4,在Rt△AOC中,OA=R,OC=R-CD=R-2,根据勾股定理得到(R-2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE.
AB=4,在Rt△AOC中,OA=R,OC=R-CD=R-2,根据勾股定理得到(R-2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE.
解:连结BE,设⊙O的半径为R,如图所示,
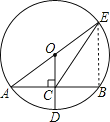
∵OD⊥AB,
∴AC=BC=![]() AB=
AB=![]() ×8=4,
×8=4,
在Rt△AOC中,OA=R,OC=R-CD=R-2,
∵OC2+AC2=OA2,
∴(R-2)2+42=R2,解得R=5,
∴OC=5-2=3,
∴BE=2OC=6,
∵AE为直径,
∴∠ABE=90°,
在Rt△BCE中,![]() .
.
考点: 1.垂径定理;2.勾股定理;3.三角形中位线定理;4.圆周角定理.
“点睛”本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:
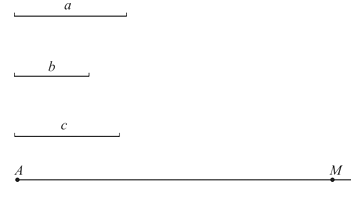
【题目】如图,已知线段a,b,c,射线AM.
(1)用圆规和直尺按要求作图(保留作图痕迹):
①用圆规在射线AM上截取AB=a;
②在射线BM上用圆规依次截取BC=b,CD=b;
③在线段DA上用圆规截取DE=c.
则线段AE= .(用a,b,c的式子表示)
(2)在(1)中所作的图形中一共能构成 条线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③同旁内角互补;④垂直于同一条直线的两条直线垂直.其中的假命题有( )
A.4 个B.3 个C.2 个D.1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图1,当点Q在DC边上时,探究PB与PQ所满足的数量关系; 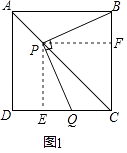
小明同学探究此问题的方法是:
过P点作PE⊥DC于E点,PF⊥BC于F点,
根据正方形的性质和角平分线的性质,得出PE=PF,
再证明△PEQ≌△PFB,可得出结论,他的结论应是
(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想. 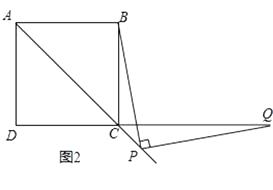
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C到AB的距离是_______,点A到BC的距离是________,点B到CD 的距离是_____,A、B两点的距离是_________.
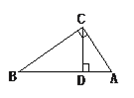
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中是随机事件的是( )
A.校运会上立定跳远成绩为10米
B.在只装有5个红球的袋中,摸出一个红球
C.慈溪市明年五一节是晴天
D.在标准大气压下,气温3°C 时,冰熔化为水
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要设计一幅长为3xcm、宽为2ycm的长方形图案,其中有两横两竖的彩条,横彩条的宽度为acm,竖彩条的宽度为bcm,问空白区域的面积是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com