
分析 在镶嵌平面时,设围绕某一点有a个正三角形和b个正六边形的内角可以拼成一个周角,根据平面镶嵌的体积可得方程:60a+120b=360.整理得:a+2b=6,求出正整数解即可.
解答 解:在镶嵌平面时,设围绕某一点有a个正三角形和b个正六边形的内角可以拼成一个周角,
根据题意,可得方程:60a+120b=360.
整理得:a+2b=6,
方程的正整数解为$\left\{\begin{array}{l}{a=2}\\{b=2}\end{array}\right.$,$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$.
所以可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌,在一个顶点周围围绕2个正三角形和2个正六边形或者围绕着4个正三角形和1个正六边形.
点评 本题考查了平面镶嵌,正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.解决此类题,可以记住几个常用正多边形的内角,及能够用两种正多边形镶嵌的几个组合.也考查了二元一次方程的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
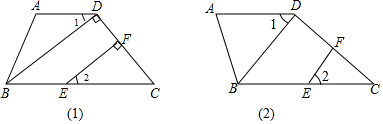
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
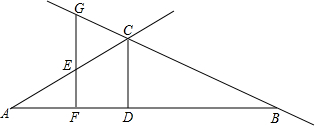 如图,已知CD⊥AB于D,E是射线AC上一动点,EF⊥AB于F,EF交直线BC于G,若∠AEF=∠CGE.
如图,已知CD⊥AB于D,E是射线AC上一动点,EF⊥AB于F,EF交直线BC于G,若∠AEF=∠CGE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
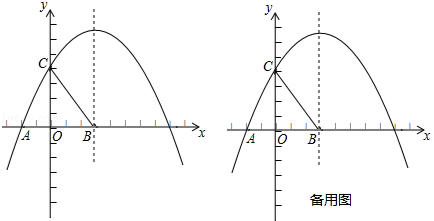
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
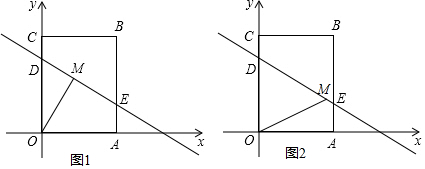
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com