
分析 甲与乙合做的工作效率为$\frac{1}{a}$,甲的工作效率为$\frac{1}{b}$,所以乙的工作效率为$\frac{1}{a}$-$\frac{1}{b}$,然后用工作总量除以乙的工作效率即可得到乙单独做需要的天数.
解答 解:甲的工作效率为$\frac{1}{b}$,则乙的工作效率为$\frac{1}{a}$-$\frac{1}{b}$=$\frac{b-a}{ab}$,
所以乙单独做需要的时间=$\frac{1}{\frac{b-a}{ab}}$=$\frac{ab}{b-a}$(天).
点评 本题考查了列代数式(分式):把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式. 本题的关键是表示出乙的工作效率.


科目:初中数学 来源: 题型:解答题
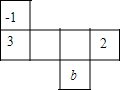 若x=1是方程$\frac{2a+x}{3}$-$\frac{x-bx}{6}$=1的解.
若x=1是方程$\frac{2a+x}{3}$-$\frac{x-bx}{6}$=1的解.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
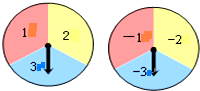 如图,有转盘A、B分别被分成三个面积相等的扇形,上面分别写有3个数字,用力转动两个转盘,转盘上的指针分别指向一个数字,则两个转盘指针指向的两个数之和恰好为0的概率是$\frac{1}{3}$.
如图,有转盘A、B分别被分成三个面积相等的扇形,上面分别写有3个数字,用力转动两个转盘,转盘上的指针分别指向一个数字,则两个转盘指针指向的两个数之和恰好为0的概率是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
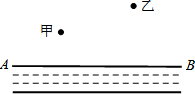 小河AB的同旁有甲、乙两个村庄,现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.若要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?(要求:不写作法,但要保留作图痕迹,并写出作图结果)
小河AB的同旁有甲、乙两个村庄,现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.若要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?(要求:不写作法,但要保留作图痕迹,并写出作图结果)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com