

���� ��1����ֱ��l��y�ύ�ڵ�C���ֱ����M��N��MA��X���ڵ�A��MB��x���ڵ�B�����ɵõ�����MAOC������NBOC�����þ��ε����ʼ�������������k�ļ����������á�MON�����Ϊ��|-1|+|2|����2=$\frac{3}{2}$�����ɵý⣻��2����ֱ��l��y=a����֪��M���N��������Ϊa��Ȼ���ʾ��������꣬�Ӷ�����߶�MN�ij��ȣ���Ϊy=aƽ����x�ᣬֱ��y=-1ƽ����x�ᣬ�ʿ����MN�ϵĸߵij��ȣ��Ӷ��ɵá�PMN����������ɽ�𣻣�3������MNΪֱ����ԲԲ��Ϊ��E������E��x��Ĵ��߶Σ�����ΪF����ԲE��x���н���ʱ����MPN�п�����һ��ֱ�ǣ��������ֱ����Բ��λ�ù�ϵ�����ɵõ��𰸣�
��� �⣺��1����ͬѧ˵����ȷ����MON�������$\frac{3}{2}$��
���ɣ���ͼ1����ֱ��l��y�ύ�ڵ�C���ֱ����M��N��MA��X���ڵ�A��NB����
���ı���MAOC�Ǿ��Σ��ı���NBOC�Ǿ���
��S��MAO=S��MCO=$\frac{1}{2}$��S��NBO=S��NCO=1��
���MON�����=$\frac{1}{2}$+1=$\frac{3}{2}$��
��2����ͬѧ˵����ȷ����PMN�����Ϊ$\frac{3}{2}$+$\frac{3}{2a}$
���ɣ���ͼ2���ߵ�M��N��ֱ��y=a�ϣ�
���M��������Ϊa����N��������Ϊa��
���M��������-$\frac{1}{a}$��a������N��������$\frac{2}{a}$��a��
���߶�MN�ij���Ϊ$\frac{3}{a}$
��y=aƽ����x�ᣬֱ��y=-1ƽ����x�ᣬ
���MN�ϵĸ�Ϊa+1��
���PMN�����=$\frac{\frac{3}{a}����a+1��}{2}$=$\frac{3}{2}$+$\frac{3}{2a}$��
��3����ͼ3������MNΪֱ����ԲԲ��Ϊ��E������E��EF��x�ᣬ����ΪF��
�ߵ�P��x���ϵ�һ�㣬
�൱ԲE��x���н���ʱ����MPN�п�����һ��ֱ�ǣ�
�ɣ�2��֪�߶�MN�ij���Ϊ$\frac{3}{a}$��
��ԲE�İ뾶Ϊ$\frac{3}{2a}$��
��y=aƽ����x�ᣬEF��x�ᣬ
��EF=a��
�൱EF��rʱ��ԲE��x���н��㣬
��ֱ��l��x����Ϸ���
��0��a��$\frac{3}{2a}$��
��0��a��$\frac{\sqrt{6}}{2}$��
���Ե�a����0��a��$\frac{\sqrt{6}}{2}$ʱ����MPN�п�����һ��ֱ�ǣ�
���� ������Ҫ���鷴����������ϵ��k�ļ������壬�����ϵ�����꣬�����ε������ֱ����Բ��λ�ù�ϵ������������ѧ֪ʶ�����ҵ�����ķ����ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 48cm | B�� | 54cm | C�� | 56cm | D�� | 64cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ������Rt��ABC�У�DΪAC��һ�㣬AE��BC��BD�ӳ�����E��AN��BE��N����BE�Ͻ�ȡMB=AN����M��MF��BE��AC�ӳ�����F����֤��CF=BC��
��֪����ͼ������Rt��ABC�У�DΪAC��һ�㣬AE��BC��BD�ӳ�����E��AN��BE��N����BE�Ͻ�ȡMB=AN����M��MF��BE��AC�ӳ�����F����֤��CF=BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�D��E�ֱ���AC��AB�ϵĵ㣬��CD=BE��BD��CE�ཻ�ڵ�P��APƽ�֡�BAC����֤��AB=AC��
��ͼ����ABC�У�D��E�ֱ���AC��AB�ϵĵ㣬��CD=BE��BD��CE�ཻ�ڵ�P��APƽ�֡�BAC����֤��AB=AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�E��AFƽ�֡�BAC����BD�ڵ�F����֤��EF+AE=AB��
��֪����ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�E��AFƽ�֡�BAC����BD�ڵ�F����֤��EF+AE=AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڵȱߡ�ABC�У�MΪBC��������һ�㣨����B��C���㣩��PΪBC�ӳ�����һ�㣬N�ǡ�ACP��ƽ������һ�㣮��֪��AMN=60�㣬��֤��AM=NM��
��ͼ���ڵȱߡ�ABC�У�MΪBC��������һ�㣨����B��C���㣩��PΪBC�ӳ�����һ�㣬N�ǡ�ACP��ƽ������һ�㣮��֪��AMN=60�㣬��֤��AM=NM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
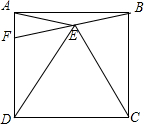 ��ͼ��E��������ABCD��һ�㣬��CDE�ǵȱ������Σ�����EB��EA���ӳ�BE��AD���ڵ�F�����AFB�Ķ����ǣ�������
��ͼ��E��������ABCD��һ�㣬��CDE�ǵȱ������Σ�����EB��EA���ӳ�BE��AD���ڵ�F�����AFB�Ķ����ǣ�������| A�� | 45�� | B�� | 60�� | C�� | 80�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
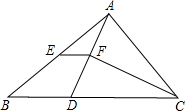 ��֪����ͼ���ڡ�ABC�У�CFƽ�֡�ACB��CA=CD��AE=EB����֤��EF=$\frac{1}{2}$BD��
��֪����ͼ���ڡ�ABC�У�CFƽ�֡�ACB��CA=CD��AE=EB����֤��EF=$\frac{1}{2}$BD���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com