
 )三点.
)三点.
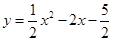 ;
; );
); ),(2+
),(2+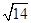 ,
, )或(2-
)或(2-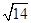 ,
, ).
). )三点代入求出a、b、c的值即可;
)三点代入求出a、b、c的值即可; )三点在抛物线上,
)三点在抛物线上, ,
, .
.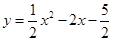 ;
;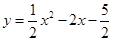 ,
,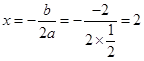 ,
,
 ),
),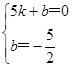 ,
,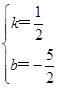 ,
,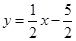 ,
, =-
=- ,
, );
);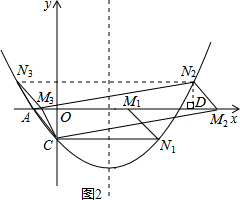
 ),∴N1(4,-
),∴N1(4,- )
)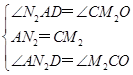 ,
, ,即N2点的纵坐标为
,即N2点的纵坐标为 .
. ,
,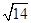 或x=2-
或x=2-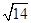 ,
,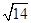 ,
, ),N3(2-
),N3(2-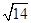 ,
, ).
). ),(2+
),(2+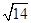 ,
, )或(2-
)或(2-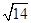 ,
, ).
).

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:不详 题型:解答题
 经过点A(3,2),B(0,1)和点C
经过点A(3,2),B(0,1)和点C .
. ,求点F的坐标;
,求点F的坐标;

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的一元二次方程
的一元二次方程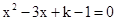 有实数根,
有实数根,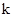 为正整数.
为正整数.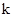 的值;
的值; 的二次函数
的二次函数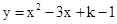 的图象向下平移2个单位,求平移后的函数图象的解析式;
的图象向下平移2个单位,求平移后的函数图象的解析式; 轴左侧的部分沿
轴左侧的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线
轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线 与图象G有3个公共点时,请你直接写出
与图象G有3个公共点时,请你直接写出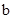 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.7.07cm2 |
| B.3.53cm2 |
| C.14.13cm2 |
| D.10.60cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com