
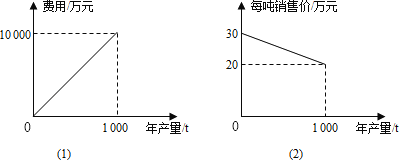
【题目】某种产品的年产量不超过1 000t,该产品的年产量(t)与费用(万元)之间的函数关系如图(1);该产品的年销售量(t)与每吨销售价(万元)之间的函数关系如图(2).若生产出的产品都能在当年销售完,则年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣费用)
【答案】(1)y=10t,(2)年产量是500吨时,当年可获得7500万元毛利润.
【解析】首先根据图象(1)(2)分别写出生产费用与年产量、每吨销售价与年销售量的函数关系式,然后根据销售额-生产费用=毛利润7500万元,列出方程,求解即可.
解:设年产量为t吨,费用为y(万元),每吨销售价为z(万元),则0≤t≤1000,
由图(1)可求得y=10t,
由图(2)求得z=﹣![]() t+30.
t+30.
设毛利润为w(万元),
则w=tz﹣y=t(﹣![]() t+30)﹣10t=﹣
t+30)﹣10t=﹣![]() t2+20t.
t2+20t.
∴﹣![]() t2+20t=7500,
t2+20t=7500,
∴t2﹣2000t+750000=0,
解得t1=500,t2=1500(不合题意,舍去).
故年产量是500吨时,当年可获得7500万元毛利润.
“点睛”本题已知信息由两个图象提供,图(1)与图(2)都是线段,看懂两图,理解关系式:毛利润=销售额-费用是解决本题的关键.由于在图象中提供的数据已满足求两个图象解析式的需要,故两个解析式均可求.本题易错在不注意销售额与销售单价的关系,而盲目地用w=z-y(销售单价-费用).


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
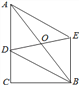
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )
A. 4 B. 2![]() C. 2 D. 6
C. 2 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+3上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
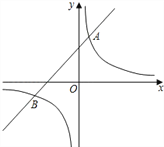
【题目】如图,一次函数y=x+1与反比例函数y=![]() 的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).
的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).
(1)求此反比例函数的解析式;
(2)当一次函数y=x+1的值大于反比例函数y=![]() 的值时,求自变量x的取值范围.
的值时,求自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com