
 经过点A(4,0),B(2,2),连结OB,AB.
经过点A(4,0),B(2,2),连结OB,AB.
 、
、 的值;
的值;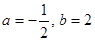 ;(2)证明见解析;(3)点
;(2)证明见解析;(3)点 不在抛物线上.
不在抛物线上.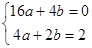 ,
,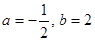 ;
;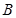 作
作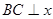 轴于点
轴于点 ,则
,则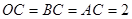 ,
,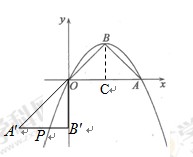
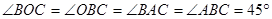 ,
, ,
, 是等腰直角三角形;
是等腰直角三角形; 是等腰直角三角形,
是等腰直角三角形,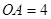 ,
, ,
,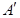 坐标为
坐标为 ,
, 的中点
的中点 的坐标为
的坐标为 ,
,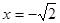 时,
时,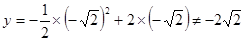
 不在抛物线上.
不在抛物线上.

 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源:不详 题型:解答题

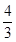 x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?
x-4的图象与x轴交于点A,与y轴交于点B,P为抛物线上的一个动点,过点P作PQ∥y轴交直线AB于点Q,以PQ为直径作圆交直线AB于点D.设点P的横坐标为n,问:当n为何值时,线段DQ的长取得最小值?最小值为多少?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 轴建立直角坐标系,桥洞上沿形状恰好是抛物线
轴建立直角坐标系,桥洞上沿形状恰好是抛物线 的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.
的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 分别与y轴、x轴相交于A、B两点,与二次函数
分别与y轴、x轴相交于A、B两点,与二次函数 的图像交于A、C两点.
的图像交于A、C两点.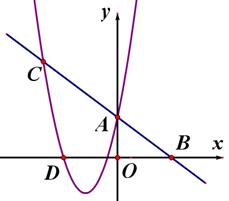
 ,
,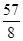 )时,求直线AB的解析式;
)时,求直线AB的解析式;  的图像上,求点D到直线AB的距离;
的图像上,求点D到直线AB的距离; 有最小值-3,求实数m的值.
有最小值-3,求实数m的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交
的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交 轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
 轴上的点(0,6)时,求此时D点的坐标;
轴上的点(0,6)时,求此时D点的坐标;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 或
或 .其中正确的是( )
.其中正确的是( )
| A.①② | B.①④ | C.②③ | D.③④ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
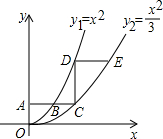
 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com