
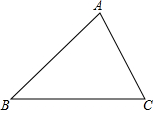
 如图,已知△ABC中,AB=4,AC=3.
如图,已知△ABC中,AB=4,AC=3.分析 (1)画出∠BAC的平分线AD即可;
(2)首先证明EA=ED,设EA=ED=x,由DE∥AC,推出△BED∽△BAC,推出$\frac{BE}{BA}$=$\frac{DE}{AC}$,列出方程即可解决问题;
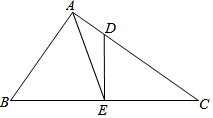
解答 解:(1)∠BAC的平分线如图所示.
(2)∵AD是∠BAC的平分线,
∴∠EAD=∠CAD,
∵DE∥AC,
∴∠ADE=∠DAC,
∴∠EAD=∠EDA,
∴EA=ED,设EA=ED=x,
∵DE∥AC,
∴△BED∽△BAC,
∴$\frac{BE}{BA}$=$\frac{DE}{AC}$,
∴$\frac{4-x}{4}$=$\frac{x}{3}$,
∴x=$\frac{12}{7}$,
∴DE=$\frac{12}{7}$.
点评 本题考查基本作图、平行线的性质、等腰三角形的判定、相似三角形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
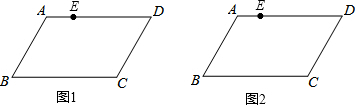
 如图,在菱形ABCD中,对角线AC、BD相交于点O,点E、F分别是边AB、BC的中点,连接EF,若EF=3,BD=6$\sqrt{3}$,则菱形ABCD的面积为( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,点E、F分别是边AB、BC的中点,连接EF,若EF=3,BD=6$\sqrt{3}$,则菱形ABCD的面积为( )| A. | 6$\sqrt{3}$ | B. | 9$\sqrt{3}$ | C. | 18$\sqrt{3}$ | D. | 36$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.
如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于78.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).
某中学初三年级的同学参加了一项节能的社会调查活动,为了了解家庭用电的情况,他们随即调查了某地50个家庭一年中生活用电的电费支出情况,并绘制了如下不完整的频数分布表和频数分布直方图(费用取整数,单位:元).| 分组/元 | 频 数 | 频 率 |
| 1000<x<1200 | 3 | 0.060 |
| 1200<x<1400 | 12 | 0.240 |
| 1400<x<1600 | 18 | 0.360 |
| 1600<x<1800 | a | 0.200 |
| 1800<x<2000 | 5 | b |
| 2000<x<2200 | 2 | 0.040 |
| 合计 | 50 | 1.000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如
如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如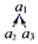 ,表示a1=a2+a3,则a1的最小值为( )
,表示a1=a2+a3,则a1的最小值为( )| A. | 32 | B. | 36 | C. | 38 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com