
 如图,下列条件不能判定△ABD∽△CBA的是( )
如图,下列条件不能判定△ABD∽△CBA的是( )| A. | ∠BAD=∠C | B. | ∠ADB=∠BAC | C. | AB2=BD•BC | D. | $\frac{BD}{AB}$=$\frac{AB}{AC}$ |
分析 由∠B是公共角,利用有两角对应相等的三角形相似,即可得A与B正确;又由两组对应边的比相等且夹角对应相等的两个三角形相似,即可得C正确,继而求得答案,注意排除法在解选择题中的应用.
解答 解:∵∠B是公共角,
∴当∠ABD=∠C或∠ADB=∠BAC时,△ABD∽△CBA(有两角对应相等的三角形相似);
故A与B正确;
当$\frac{AB}{BC}=\frac{BD}{AB}$时,即AB2=BD•BC,则△ABD∽△CBA(两组对应边的比相等且夹角对应相等的两个三角形相似);
故C正确;
当$\frac{BD}{AB}=\frac{AB}{AC}$时,∠B不是夹角,故不能判定△ABD与△CBA相似,故D错误.
故选D.
点评 此题考查了相似三角形的判定.此题难度不大,注意掌握有两角对应相等的三角形相似与两组对应边的比相等且夹角对应相等的两个三角形相似定理的应用.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
 如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直.马路宽20米,A,B相距62米,∠A=67°,∠B=37°.
如图,马路的两边CF,DE互相平行,线段CD为人行横道,马路两侧的A,B两点分别表示车站和超市.CD与AB所在直线互相平行,且都与马路的两边垂直.马路宽20米,A,B相距62米,∠A=67°,∠B=37°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
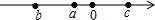 已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$-$\sqrt{(a-c)^{2}}$-$\sqrt{(b-c)^{2}}$的结果是( )
已知实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$-$\sqrt{(a-c)^{2}}$-$\sqrt{(b-c)^{2}}$的结果是( )| A. | -3a | B. | -a+2b-2c | C. | 2b | D. | a |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点A、B在双曲线y=$\frac{m}{x}$(m>0)上,点C、D在双曲线y=$\frac{n}{x}$(n<0)上,
如图,已知点A、B在双曲线y=$\frac{m}{x}$(m>0)上,点C、D在双曲线y=$\frac{n}{x}$(n<0)上,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,函数y=-3x和y=kx+b的图象相交于点A(m,4),则关于x的不等式kx+b+3x>0的解集为x>-$\frac{4}{3}$.
如图,函数y=-3x和y=kx+b的图象相交于点A(m,4),则关于x的不等式kx+b+3x>0的解集为x>-$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数 | 2 | 4 | 3 | 1 |
| A. | 16,14 | B. | 14,14 | C. | 14,15 | D. | 15,14 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com